Line dividing a triangle

The workings:

As every year, the amusement section takes a well-deserved break for a few weeks, but not without once again offering our readers a special problem to liven up lazy summer afternoons.

The fun:

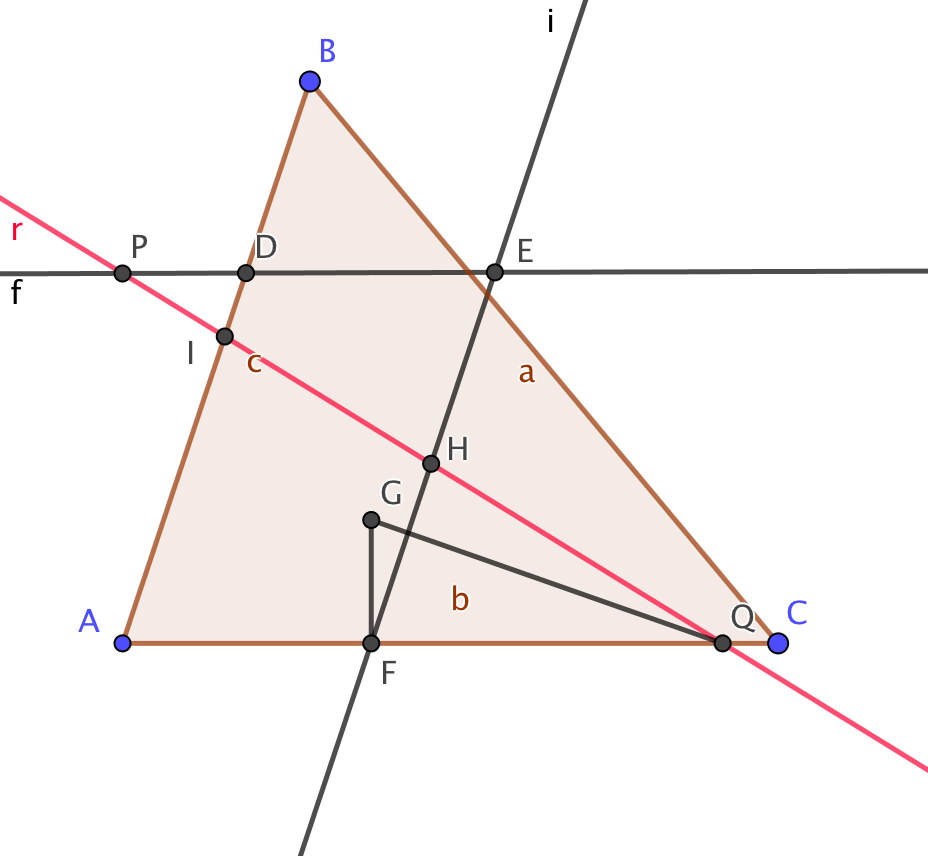
Those of us who thought of including in our blog a section in which to pose problems for the entertainment of our readers, give the solution in a few days and pay tribute to those who, in addition to solving them, submit their solution, cannot boast of being original. This is a practice with a long tradition in mathematical magazines. In a more than centenary issue of a well-known monthly magazine, founded in the 19th century, we find the following problem: Given a triangle ABC and a point P, draw a line through P and divide the triangle into two surfaces of equal area. One of the solutions submitted and accepted by the editorial staff read as follows: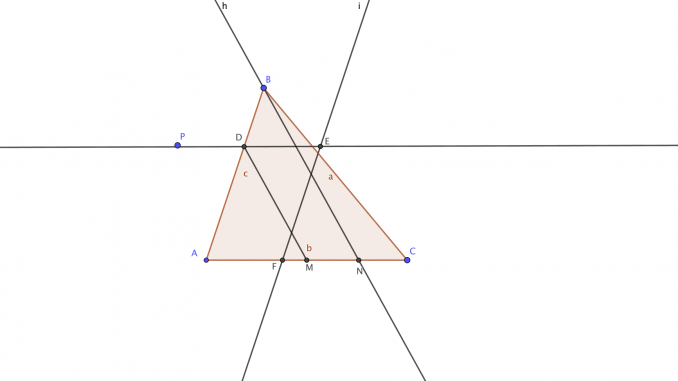

1. Draw through P a parallel to AC that cuts the first side of the triangle it meets, AB in the drawing, at D.
2. Join D with the midpoint M of AC. Draw through B a parallel to the line DM, which cuts AC at N.
3. Find the midpoint F of AN.
4. Draw a parallel through F to the side on which D lies, meeting the line PD at E.
5. Draw the auxiliary quadrilateral ADEF.
6. A perpendicular to AC is drawn through F, and G is determined such that FG=PD.
7. With G as centre, draw an arc of radius PE that cuts AC at Q.
8. The line PQ is the line we are looking for.

Given this, we ask our readers:

1. Justify that the area of the parallelogram AFED is half the area of ABC.
2. Justify the construction.
3. This construction cannot be made from every point P in the plane. Indicate from which of them it is possible to do it.

.

.

.

.

.

.

Solutions

We encourage the readers to try to solve the divertimento for themselves. Whether you succeed or not, you can always consult the solution in this link.