Solution: line dividing a triangle

We publish here the solution to the divertimento Line dividing a triangle.

The fun:

Those of us who thought of including in our blog a section in which to pose problems for the entertainment of our readers, give the solution in a few days and pay tribute to those who, in addition to solving them, submit their solution, cannot boast of being original. This is a practice with a long tradition in mathematical magazines. In a more than centenary issue of a well-known monthly magazine, founded in the 19th century, we find the following problem:

Given a triangle ABC and a point P, draw a line through P and divide the triangle into two surfaces of equal area.

One of the solutions submitted and accepted by the editorial staff read as follows:

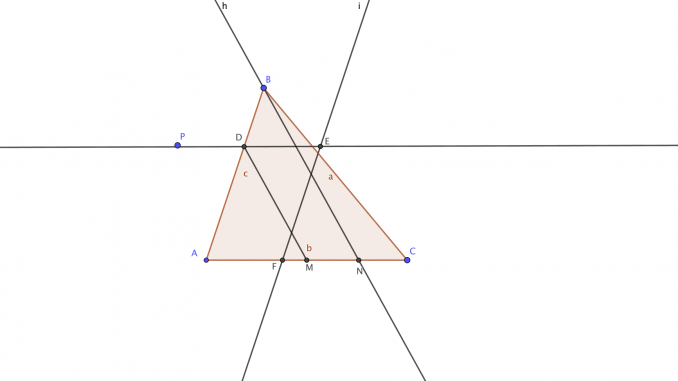
1. Draw through P a parallel to AC that cuts the first side of the triangle it meets, AB in the drawing, at D.
2. Join D with the midpoint M of AC. Draw through B a parallel to the line DM, which cuts AC at N.
3. Find the midpoint F of AN.
4. Draw a parallel through F to the side on which D lies, meeting the line PD at E.
5. Draw the auxiliary quadrilateral ADEF.
6. A perpendicular to AC is drawn through F, and G is determined such that FG=PD.
7. With G as centre, draw an arc of radius PE that cuts AC at Q.
8. The line PQ is the line we are looking for.

Given this, we ask our readers:

1. Justify that the area of the parallelogram AFED is half the area of ABC.
2. Justify the construction.
3. This construction cannot be made from every point P in the plane. Indicate from which of them it is possible to do it.

The solution:

(1) Indeed, the triangles \(ADM\) and \(ABN\) are similar, so that if we denote \(h\) and \(h_1\) the respective heights of ABN (or ABC) and of ADM, we will have $$\frac{AM}{AN}=\frac{h_1}{h}, \qquad AM \cdot h = AN \cdot h_1.$$ Then the area of the rectangle \(ADEF\) es $$S(ADEF)=AF \cdot h_1= \frac{1}{2} AN \cdot h_1 =\frac{1}{2} AM \cdot h  = \frac{1}{2}S(ABC).$$

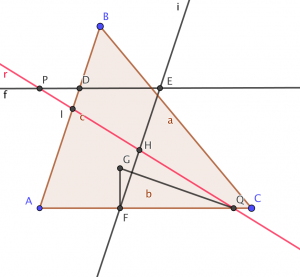
(2) In figure 2, the triangles \(FHQ\) and \(EHP\) are similar and so are the triangles \(PID\) and \(PHE\). So that it is satisfied that $$\frac{S(FHQ)}{S(EHP)}=\left( \frac{FQ}{PE} \right)^2, \qquad \frac{S(PID)}{S(EHP)}=\left( \frac{PD}{PE} \right)^2.$$ Then $$\frac{S(FHQ)}{S(EHP)}=\frac{FQ^2}{PE^2}=\frac{PE^2-PD^2}{PE^2}=1-\frac{S(PID)}{S(EHP)}.$$ Therefore $$S(FHQ)=S(EHP)-S(PID)=S(DEHI),$$ and so $$S(AIQ)=S(AIHF)+S(DEHI)=S(ADEF)=\frac{1}{2}S(ABC).$$

(3) The previous construction needs two conditions: that the parallel to a side drawn by the point \(P\) cuts the other two sides and that the point \(Q\) falls inside the side of the triangle and not on its prolongation.

Suppose then that the parallel through \(P\) to \(AC\) meets the other two sides. We set up a reference frame so that the coordinates of the three vertices of the triangle are \(A(a,0)\), \(B(0,b)\) and \(C(c,0)\). The coordinates of \(P\) will be \(P=(x_0,y_0)\), and therefore \(0<y_0<b\). We place the vertices \(A\) and \(C\) so that the point \(P\) is in a different half-plane from the triangle with respect to the line \(AB\) and in the same with respect to the line \(BC\). Thus, it can be proved that:

• The point \(D\) is $$ D=\left(a – \frac{a}{b}y_0,  y_0\right)$$
• The point \(M\) is $$ M=\left(\frac{a+c}{2}, 0\right)$$
• The point \(N\) is $$ N=\left(a – \frac{(a-c)b}{2y_0}, 0\right)$$
• The point \(F\) is $$ F=\left(a – \frac{(a-c)b}{4y_0},  0\right)$$
• The point \(E\) is $$ E=\left(a – \frac{a}{b}y_0 + \frac{(a-c)b}{4y_0},  y_0\right)$$
• The distance \(PD\) is $$ PD=\left| a- \frac{a}{b}y_0-x_0 \right|$$
• The distance \(PE\) is $$ PE=\left| a- \frac{a}{b}y_0+ \frac{(c-a)b}{4y_0}-x_0 \right|$$
• The distance \(CF\) is $$ PE=\left| a+ \frac{(c-a)b}{4y_0}-c \right|$$

The condition to verify is $$PE^2 -PD^2 \leq CF^2,$$ that is, $$\begin{cases} bx_0+(2c-a)y_0 \geq bc, & \text{if } a<0,c>0 \\ bx_0+(2c-a)y_0 \leq bc, & \text{if } a>0,c<0\end{cases}.$$ It can be verified that the line $$bx+(2c-a)y=bc$$ passes through the points \((c,0)\) and \((a/2,b/2)\) and therefore it is the median from the vertex \(C\). The domain where \(P\) can be placed so that the previous construction is possible is, then, the one bounded above by the parallel to \(AC\) that passes by \(B\) and below by the median from \(C\). When the construction is carried out on the three sides, it turns out

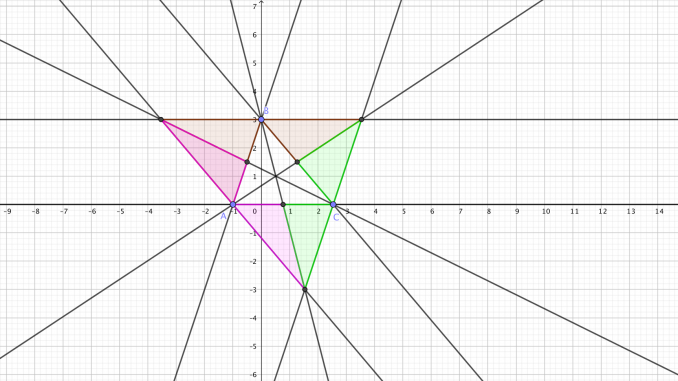
where the points of the brown triangles must begin on the parallel to \(AC\), those of the purple triangles begin on the parallel to \(BC\) and those of the green triangles begin on the parallel to \(AB\).

(Taken in part from American Mathematical Monthly, Vol 16, no. 8-9 (1909))