Halle Berry and the control of diabetes

This post aims to show how certain mathematical techniques can help in the difficult task of the medical treatment of diabetes.

Let us start by talking about Halle Berry, the famous actress who starred (among others) in the film “Seducing a Stranger” (2006). In 2002, she became the first black actress to win the Oscar for Best Actress for her role in “Monster’s Ball”.

Halle Berry was diagnosed with type 1 diabetes when she was in her early 20s. She suffered severe crises and was in a coma for several days. She recently stated that her strict adherence to a well-chosen diet had helped her to control her diabetes. Although this statement generated some controversy; we will return to it at the end of the post.

What is diabetes?

Diabetes is a chronic (long-term) disease. It affects the way the body converts food into energy.

In very simplified terms, we can say that, with most of the food eaten, the body generates glucose, which is released into the blood. In a second stage, thanks to a hormone produced by the pancreas, called insulin, the blood sugar enters the cells and the cells convert it into energy.

There are three types of diabetes: in a type 1 patient, not enough insulin is produced; on the other hand, patients with type 2 diabetes are characterised by the fact that the insulin produced does not adequately fulfil its function; there is also gestational diabetes, which affects pregnant women who have never had diabetes (it usually disappears after childbirth). In all cases, there is an excess of sugar in the blood and this can and often does cause serious health problems: heart disease, loss of vision, kidney disease, etc.

Type 1 diabetes is mainly diagnosed in children, adolescents and young adults. Generally, people with type 1 diabetes must take insulin (injected or pumped) every day in order to survive. At present, no one knows how to prevent or cure type 1 diabetes; it is said to be a non-curable but controllable disease.

The insulin pump is a device that allows insulin to be administered continuously. It consists of an infuser (a micro-computer previously programmed to properly deliver insulin) and a catheter that connects the pump to the subcutaneous tissue.

Type 2 diabetes affects more than 90% of diabetics. It is usually diagnosed in adults and can be prevented or delayed with lifestyle changes: weight loss, healthy eating, regular physical activity, etc.

In 2019, some 463 million people had diabetes worldwide. The percentage of adults with diabetes was 9.3% (the countries with the highest percentage were Germany and Mexico, respectively with 15.3 and 15.2). In Spain, the estimated number of diabetics was 3.6 million, 10.5% of the adult population.

The term “diabetes mellitus”, rather than simply “diabetes”, is often used to distinguish this disease from “diabetes insipidus”, a relatively rare disorder characterised by the inability of the kidneys to prevent the elimination of water.

For more information, see for example [1, 2].

Celebrities with diabetes

The list of celebrities that have been affected by this disease is long. Let us mention a few of them:

– Elvis Presley: As far as is known, he was not diagnosed during his lifetime but an autopsy performed after his death in 1977 confirmed that he suffered from diabetes.

– Tom Hanks: This actor admitted to having been diagnosed in 2013, yet had been dismissive of the symptoms for years. He now leads a much healthier life.

– Salma Hayek: Salma, now 56, had never had any problems with her blood sugar levels until she became pregnant at the age of 41. At that time she was diagnosed with gestational diabetes.

– Carlos Sobera (Spanish showman and comedian): He has had diabetes since 2011. Since then, he has wanted to make the disease as visible as possible.

– Nacho Fernández Iglesias: Nacho, a Real Madrid footballer, has had type 1 diabetes since the age of 12. He has said that he has to take special care of himself, but that does not prevent him from successfully practising his profession.

What can mathematics do to help a diabetic?

Mathematics provides tools that make it possible to describe and understand the evolution of the disease and, potentially, to obtain meaningful data. Even better, there are also tools that make it possible to determine optimal or at least effective therapies.

I will now describe one way of approaching the treatment of the problem from among the many existing possibilities:

\(\bullet\) We define the following functions \(x_i = x_i(t)\) for \(t \in [0,T]\):

\((x_1,x_2)\) (resp. \((x_3,x_4)\)): blood plasma concentrations (resp. intracellular concentrations) of glycogen and insulin.

\((x_5,x_6)\): glycogen and insulin receptor concentrations.

\((x_7,x_8)\): blood concentrations of glycogen and glucose.

\((x_9,x_{10})\): rate of oxygen consumption and ‘clean’ (due to oxygen) insulin.

\(\bullet\) We consider a system of equations satisfied by the \(x_i\), where (for simplicity) I will only detail the first two and last two:

\(x_1′ = -\alpha_1 x_1 + G_m(1-b_1 e^{a_1(x_8-C_5)})^{-1}\)

\(x_2′ = -\alpha_2 x_2 + R_m(1-b_2 e^{a_2(C_1-x_8)})^{-1} + \sum_{j=0}^M I(t;D_j,T_j)\)

\(\dots\)

\(x_9′ = \gamma(u_{ex}(t)-x_9), \ \ x_{10}’ = \eta x_9 – \mu x_{10}\)

These equations contain positive constants \(\alpha_i\), \(G_m\), \(a_i\), etc., which correspond to the interaction of the different components. In particular, the case \(R_m = 0\) (resp. \(R_m > 0\)) corresponds to type 1 diabetes (resp. type 2).

The function \(I = I(t;D,T)\) has a relatively complex expression; \(I(t;D,T)\) determines for each \((t;D,T)\) the increase at the instant \(t\) of the blood plasma glucose concentration produced by a dose of \(D\) units of insulin applied at the instant \(T\).

Other data that depend on the external action arise: on the one hand, the insulin doses \(D_j\) and the application times \(T_j\) (with \(j = 1, \dots, M\)); on the other hand, the oxygen supply \(u_{ex} = u_{ex}(t)\) caused by physical exercise.

Knowing these data and prescribed initial values for the \(x_i\) (i.e. values for \(t=0\)), it is possible to determine with high precision the values of the \(x_i\) concentrations at all times \(t \in [0,T]\). In this way, we will be able to measure the blood glucose concentration \(x_8\) over the entire time interval.

\(\bullet\) On the other hand, we formulate the following optimal control problem:

$$
\left\{
\begin{array}{l}\displaystyle
\hbox{Minimise }\ \int_0^T |x_8(t) – g_d(t)|^2 \,dt
\\ \displaystyle
\hbox{Subject to }\ u_{ex} \in L^2(0,T), \ \ 0\leq u_{ex} \leq u_{max}, \ \ 0 \leq T_j \leq T, \ \ 0\leq D_j \leq D_{j,max} \,,
\end{array}
\right.
$$
where \(g_d = g_d(t)\) is a given function (the desired blood glucose concentration), \(u_{max} = u_{max}(t)\) is a function that determines the maximum of oxygen accepted by the body at each \(t\) and the \(D_{j,max}\) are maximum values allowed for the insulin doses administered.

It is possible to prove that there exists at least one solution to this problem. This means that there are optimal ways of administering insulin (optimal doses and optimal timing) and optimal ways of regulating oxygen supply (i.e. optimal exercise planning). By ”optimal” we mean those measures that bring the \(x_8\) distribution of blood glucose closer to the target distribution \(g_d\) than any other.

It can also be shown that any solution \((\hat{u}_{ex}, \hat{T}_1, \dots, \hat{T}_M, \hat{D}_1, \dots, \hat{D}_M)\) (i.e. any optimal control) must satisfy an appropriate optimality system. More precisely, there exist functions \(\hat{y}_1, \dots, \hat{y}_{10}\) such that, the optimal control, the corresponding solution \(\hat{x}_1, \dots, \hat{x}_{10}\) (i.e. the associated state) and the \(\hat{y}_i\) satisfy a complicated system of \(21 + 2M\) equations that can be used to compute in closed loop the optimal control.

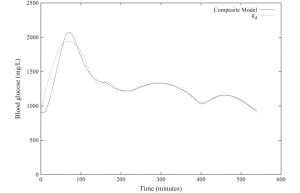
A collection of numerical experiments corresponding to realistic situations showing the usefulness of these techniques can be found in [3]. We present in Figure 8 the evolutions of the \(g_d\) function and of the \(8\)-th component of the state (the computed optimal blood glucose concentration) when \(M = 5\) (\(5\) insulin doses are accepted) and the patient performs physical exercise. It is observed that the “final” values \(\hat{x}_8(T)\) and \(g_d(T)\) are close, although not coincident.

There are many interesting issues related to the control of the previous system. For example, given initial data for the \(x_i\) and a desired final data \(x_8^T > 0\), we can ask whether there exist doses \(D_j\), times \(T_j\) and admissible functions \(u_{ex} = u_{ex}(t)\) such that \(x_8(T) = x_8^T\) (if this is the case, the system is said to be partially controllable).

As far as I know, this problem is open. Perhaps, the techniques in [4, 5] can help to solve it.

Note that, if we knew how to give a complete answer, that is, if we were able to compute the values of the \(D_j\), the \(T_j\) and \(u_{ex}\) that make \(x_8(T) = x_8^T\), we would have found a “cure” for the disease.

Let us go back to Halle Berry. The diet she follows is popularly known as the “keto diet”. It is a ketogenic eating regime, i.e. an eating plan based on increasing fat intake and decreasing carbohydrate intake. This programme is believed to reduce insulin intake while keeping blood glucose levels stable. However, a large part of the medical community is very sceptical about this.

It would be interesting to generate a model where the effect of the diet is reflected and compare the values of the variable \(x_8\) associated (for example) with the keto diet with those provided, without diet prescription, by different levels of insulin administration.

Learn more

1. https://www.mayoclinic.org/es-es/diseases-conditions/diabetes/symptoms-causes/syc-20371444
2. https://es.wikipedia.org/wiki/Diabetes_mellitus
3. Z. Al Helal, V. Rehbock , R, Loxton, “Insulin injections and exercise scheduling for individuals with diabetes: An optimal control model”, Optimal Control, App. and Methods, Vol. 39, No. 2, 2017.
4. J.-M., Coron, “Control and Nonlinearity”, Mathematical Surveys and Monographs, 136. American Mathematical Society, Providence, RI, 2007.
5. S.S. Hacisalihzade, “Biomedical applications of control engineering”, Lecture Notes in Control and Information Sciences, 441. Springer, Heidelberg, 2013.