Physics and Mathematics
Pólya was hesitant when it came to choosing his career. He said: I thought I was not good enough for physics and I was too good for philosophy. Mathematics is in between. I also debated when I was young between studying Physics or Mathematics, but I chose Mathematics for the sake of Freedom. Physics has to explain the real world, while the mathematician is free to create a world and study it, and, if he wants to, he can study the real world. The truth is that it is not strange that many physicists end up doing mathematics, proving to have made a bad choice.
One strategy for the proof of the Riemann hypothesis is what is known as the Hilbert-Pólya conjecture. It involves finding a self-adjoint operator on a Hilbert space whose eigenvalues would be the ordinates of the zeros of the zeta function. Since the operator is self-adjoint these eigenvalues would be real. In Quantum Mechanics a system is governed by a self-adjoint operator the Hamiltonian. So they thought that a suitable physical system would have as Hamiltonian the Hilbert-Pólya dream operator. To me Classical Quantum Mechanics is a physical theory in sin. The sin of not being relativistic and the sin of not knowing well what an observation is.
Having said the above, let us return to mathematics. One has to find a Hilbert space \(H\) and an operator \(D\) on this space. Then one has to prove two things that \(D\) is self-adjoint and that the zeta zeros are all of the form \(\frac12+i\lambda\) when \(\lambda\) run through the eigenvalues of \(D\).
Alain Connes won the Fields Medal in 1982 for his work in Operator Theory. Apart from being a great mathematician he is also a theoretical physicist. We are going to comment today on a joint work with Caterina Consani. I must say that the work is interesting and contains new ideas and numerical experiments that have surprised me. There is no doubt that physical ideas have led Connes and Consani to their surprising results. But my aim here will be to expose the mathematical part of their work. I hold physics in high esteem, but this anti-physics mode I think in this case makes it very clear what is really in front of us.

Weil’s explicit formula
We must begin by explaining the equivalence of the Riemann hypothesis with the positivity of the Weil quadratic form.
Let \(\mathbb R^*_+\) be the multiplicative group of positive real numbers. The Haar measure on this group is \(\frac{dx}{x}\). For \(\varphi\in\mathcal C_c^\infty(0,+\infty)\) (space of indefinitely differentiable functions with compact support contained in \((0,+\infty)\)) we define the Fourier transform (or its Mellin transform) by $$\widehat\varphi(t)=\int_0^\infty \varphi(x) x^{-it}\frac{dx}{x}.$$
The functional equation of the zeta function tells us that \(\pi^{-s/2}\Gamma(s/2)\zeta(s)\) takes the same value in \(s\) and \(1-s\), this implies that it is real on the critical line and, therefore, the argument of the factor \(\pi^{-s/2}\Gamma(s/2)\) in the line $$\vartheta(t)=\Im\log\Gamma(\tfrac14+\tfrac{it}{2})-\frac{t}{2}\log\pi,$$ is a real function such that \(\zeta(\frac12+it)=e^{-i\vartheta(t)}Z(t)\) with \(Z(t)\in\mathbb R\). The function \(\vartheta(t)\) is a very simple and easy to compute real function. We have defined it by its role in Weil’s explicit formula. Another element we will use are the zeros \(\alpha\) of the function \(\Xi(t)\) which are such that \(\frac12+i\alpha\) are all complex zeros of the function \(\zeta(s)\). The Riemann hypothesis states that all the numbers \(\alpha\) are real.
Teorema (Weil’s explicit formula). For any \(\varphi\in \mathcal C_c^\infty(0,+\infty)\) we have $$\sum_{\Xi(\alpha)=0}\widehat\varphi(\alpha)=\widehat\varphi(\tfrac{i}{2})+\widehat\varphi(-\tfrac{i}{2})-\sum_p\sum_{m=1}^\infty \frac{\log p}{p^{m/2}}(\varphi(p^m)+\varphi(p^{-m}))+\frac{1}{\pi}\int_{-\infty}^\infty\vartheta'(t)\widehat\varphi(t)\,dt,$$ where each zero \(\alpha\) is repeated in the sum according to its multiplicity.
We define Weil’s hermitic form by $$W(\varphi_1,\varphi_2)= \sum_{\Xi(\alpha)=0}\widehat\psi(\alpha), \qquad \psi(x)=\int_0^\infty \varphi_1(t)\overline{\varphi_2(t/x)}\frac{dx}{x}.$$ The Weil’s quadratic form is defined by \(QW(\varphi)=W(\varphi,\varphi)\).
Proposition. Riemann’s hypothesis is equivalent to the positivity of the quadratic form \(QW(\varphi)\ge0\) for any \(\varphi\in\mathcal C_c^\infty(0,+\infty)\).
The hermitic form (and the corresponding quadratic form) have another expression given by the right-hand member of the explicit formula. We see that if the support of \(\varphi\) is contained in \([\lambda^{-1},\lambda]\), then the sum of the primes in \(W(\varphi,\varphi)\) only contains the primes with \(p<\lambda^2\). In particular, for \(\lambda=\sqrt{2}\) the sum over the primes is identically \(0\).
Yoshida in 1990 started the competition of proving the positivity of \(QW_\lambda\) (the restriction of \(QW\) to functions with support contained in \([\lambda^{-1},\lambda]\) for the largest possible \(\lambda>1\). Yoshida proved it for \( \lambda=\sqrt{2}\) when primes play no role. Connes-Consani play this but what interests us is what they obtained in another direction.
Computing eigenvalues of \(QW_\lambda\) directly
We want to compute the smallest eigenvalue of \(QW_\lambda\) to prove that it is \(\ge0\). It turns out that they are rather small, for example for \(\lambda^2= 11\) it is \(2.389\times10^{-48}\).
To calculate them Connes-Consani convert the problem into a discrete one.
The usual trigonometric system in \(L^2([-L/2,L/2],dx)\) $$\xi_n(x)=\begin{cases} (-1)^n (2/L)^{1/2} \cos\left(\frac{2\pi n x}{L}\right) & \text{for $n>0$},\\ L^{-1/2}, & \text{for $n=0$,}\\ (-1)^n (2/L)^{1/2} \sin\left(\frac{2\pi n x}{L}\right) & \text{for $n<0$,}\end{cases},\qquad |x|\le L/2,$$ can be transferred by the change of variables \(x\mapsto e^x\) to the space \(L^2([\lambda^{-1},\lambda],dx/x)\), with \(L/2=\log \lambda\). Therefore the functions $$\eta_n(x)=\xi_n(\log x)$$ form a complete orthonormal system in \(L^2([\lambda^{-1},\lambda],dx/x)\).
Connes-Consani take a large natural number \(N\) and consider the space \(E_N\) generated by these \(\eta_n\) functions with \(|n|\le N\). They compute the matrix \(W(\eta_n,\eta_m)\) and obtain the smallest eigenvalue of this matrix and its corresponding eigenfunction as a linear combination of the \(\eta_n\) with \(|n|\le N\).
It turns out that the matrix \((W(\eta_n,\eta_m))_{|n|, |m|\le N}\) is symmetric and its terms cancels when \(n\ge0\) and \(m<0\). So the operator decomposes into two corresponding to the odd and even functions $$\varphi(x^{-1})=\varphi(x),\qquad \varphi(x^{-1})=-\varphi(x).$$
Prolate spheroidal functions
One of the most interesting ideas of the article is to recognize the eigenfunctions obtained by the above procedure. But this is not a demonstration, but rather a heuristic reasoning followed by experimental confirmation.
Let us consider an operator \(\mathcal E\) defined on \(\mathcal S_0^{\text{ev}}\) the space of even Schwartz functions and such that \(f(0)=\widehat f(0)=0\) by the formula $$\mathcal E f(x)= \sqrt{x}\sum_{n>0}f(nx).$$ It is connected with Weil’s quadratic form by the relatively easy to prove fact that \(QW(\mathcal E f)=0\) for any \(f\in\mathcal S_0^{\text{ev}}\). The proof is straightforward using the definition of \(QW\) via the zeros of the function \(\Xi\). Given a function on the Schwartz space \(f\in\mathcal S_0^{\text{ev}}\) the Poisson formula proves that $$(\mathcal E\widehat f\;)(x)=(\mathcal E f)(x^{-1}), \qquad x>0, \quad f\in\mathcal S_0^{\text{ev}}.$$
It is natural to think that the small eigenvalues of \(QW_\lambda\) correspond to eigenfunctions where \(QW(\varphi)=0\). This is why we will look for \(\varphi=\mathcal E f\). As in the case of the \((W(\eta_n,\eta_m))\) eigenfunctions our \(\varphi\) have to be even or odd: \(\varphi(x)=\pm\varphi(x^{-1})\). These conditions and Poisson’s formula lead us to search for a function \(f_0\in \mathcal S^{\text{ev}}\) such that \(f(0)=\widehat f(0)=0\), with support in \([-\lambda,\lambda]\), such that \(\widehat f(x)\approx \pm f(x^{-1})\) for \(|x|<\lambda\) and such that \(\widehat f(x)\) is very small for \(x>\lambda\).
All this leads to the prolate spheroidal functions. These functions first appeared in Analysis as solutions of a second order differential equation that appears when transforming a differential operator to prolate spheroidal coordinates. But they owe their importance to the work of Slepian and co-workers at the Bell Telephone Company laboratories who in the 1960s discovered their role in relation to the truncated Fourier transform.
The truncated Fourier operator $$\mathcal F_\lambda\colon L^2[-\lambda,\lambda]\to L^2[-\lambda,\lambda]$$ defined by $$(\mathcal F_\lambda)(x)=\int_{-\lambda}^\lambda\varphi(t)e^{ixt},dt$$ is compact. There exists a sequence of functions (the spheroidal prolate) satisfying $$\int_{-\lambda}^{\lambda}\psi_{m,\lambda}(x) e^{2\pi i x y}\,dx=\chi_m\psi_{m,\lambda}(y).$$ The sequence of eigenvalues \(\chi_m\) tends to zero, but for each value of \(\lambda\) it starts with several eigenvalues very approximately equal to \(\chi_m\approx(-1)^m\). When \(\lambda^2\) is a half-integer the number of these eigenvalues is \(\nu(\lambda^2)\approx 2\lambda^2-1\). This corresponds to compactly supported functions whose transform is approximately also supported on the same compact.
The spheroidal prolate functions do not satisfy \(f(0)=\widehat f(0)=0\), but we get others with the same parity and satisfying this condition by putting $$\begin{aligned}\phi_{2n}(x)&=\psi_{2n}(x)\psi_0(0)-\psi_0(x)\psi_{2n}(0)\\ \phi_{2n+1}(x)&=\psi_{2n+1}(x)\psi_1(0)-\psi_1(x)\psi_{2n+1}(0) \end{aligned}$$ It is easy to compute the Fourier developments of the functions \(\mathcal E \phi_n\) $$(\mathcal E \phi_{n})(x)=\sum_{n\in\mathbb Z} a_{n,j}\eta_j(x),$$ we truncate their developments $$\begin{aligned} (\mathcal E \phi_{2n})(x)\approx\mathcal E_{2n}(x)&:=\sum_{j=0}^N a_{2n,j}\eta_j(x),\\ (\mathcal E \phi_{2n+1})(x)\approx\mathcal E_{2n+1}(x)&:=\sum_{j=1}^N a_{2n+1,-j}\eta_{-j}(x).\end{aligned}$$ And finally we orthonormalize these functions following the Gram-Schmidt process separately in the even and odd functions. In this way we obtain the functions \(\varepsilon_n(x)\) para \(2\le n\le \nu(\lambda^2)-1\). Remarkably, these \(\varepsilon_n\) functions are the eigenfunctions of the form \(QW_\lambda\) corresponding to small eigenvalues. In the graph are plotted the two eigenfunctions for \(\lambda^2\) between \(3.5\) and \(11\), in many cases the coincidence is such that only one function is visible.
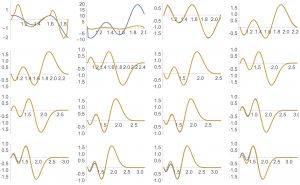
More surprises
The \(\varepsilon_n\) functions are orthonormal by construction. The first \(k\) functions \(\{\varepsilon_2,\dots,\varepsilon_{k+1}\}\) generate a subspace \(H_k\) of dimension \(k\) in \(L^2[\lambda^{-1},\lambda]\), in the space orthogonal to \(H_k\) we consider the operator \(D=-ix\frac{d}{dx}\). That is, we consider the operator $$D(\lambda,k)=(1-\Pi(\lambda,k))\circ D\circ (1-\Pi(\lambda,k)),$$ where \(\Pi(\lambda,k)\) is the projection onto the subspace \(H_k\) generated before. When \(k\) is less than but practically equal to its maximum value \(\nu(\lambda^2)-2\) we prove that the number of eigenvalues of \(D(\lambda,k)\) in the interval \((0,E]\) with \(E=2\pi \lambda^2\) is approximately $$\frac{E}{2\pi}\log\frac{E}{2\pi}-\frac{E}{2\pi},$$ as many as those of the zeta function. And if we go to the examples these eigenvalues almost coincide with those of the zeta function.
The surprising thing here is that the projection \(\Pi(\lambda,k)\) has had nothing to do with the zeta function or its zeros. We have started from the spheroidal prolate functions and with them we have constructed a space, and the \(D\) operator could not be simpler. However the coincidence with the zeros of the zeta function is very remarkable. By the way, this \(D\) operator was predicted in a previous article based on physical arguments.
There is one more surprise. Connes and Consani plot the functions \(\lambda_1(D(\lambda,k))\) of the first eigenvalue as a function of \(\lambda\).
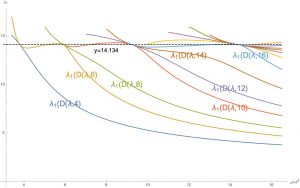
We see that these curves coincide at some points, precisely when they take the value of the ordinate of the first zero of zeta (or of the \(j\)-th if we represent \(\lambda_j(D(\lambda,k))\). The values of \(\mu=\lambda^2\) where these coincidences occur are also remarkable, precisely when \(\lambda=e^{\pi n/\gamma_1}\) with \(n\) a natural number.
Explanations
Connes Consani’s paper contains only one important theorem. But it is a theorem that gives a characterization of the real numbers \(\gamma\), such that. \(\zeta(\frac12+i\gamma)=0\). The remarkable thing, from my point of view is that it provides a difference between the zeros on the critical line and the possible zeros in the band but outside the line, that is, of the chimerical exceptions to the Riemann hypothesis.
[I use the word chimerical here because that is what most mathematicians would say, not me, I do not see its existence as so unlikely].
We introduce two other operators $$(\Sigma_\mu g)(x)=\sum_{k\in\mathbb Z}g(\mu^k x)\qquad \vartheta_\lambda f(x)= f(\lambda^{-1}x).$$ When it is defined \((\Sigma_\mu g)(\mu x)=(\Sigma_\mu g)(x)\). So we can understand that this function is defined on \(C_\mu:=\mathbb R^*_+/\mu^\mathbb Z\) this space has the topology of a circle and can be endowed with the measure \(dx/x\).
The main theorem of the article is the following characterization of zeta zeros on the critical line.
Teorema. The subspace \(\Sigma_\mathcal E (\mathcal S_0^{\text{ev}})\subset L^2(C_\mu)\) is not dense if and only if \(\mu=\exp(\frac{2\pi n}{\lambda_r})\) for \(n\in\mathbb Z\) and \(\lambda_r\) any real number such that \(\zeta(\frac12+i\lambda_r)=0\).
In the situation of the theorem we have \(x^{i\gamma_r}\in\bigl(\Sigma_\mu\mathcal E (\mathcal S_0^{\text{ev}})\bigr)^\perp\). And our operator \(D\) satisfies then $$D(x^{i\gamma_r})=-ix\frac{d}{dx}(x^{i\gamma_r})=\gamma_r x^{i\gamma_r}.$$ In the space \(\bigl(\Sigma_\mu\mathcal E (\mathcal S_0^{\text{ev}})\bigr)^\perp\) the operator \(D\) has as an eigenfunction \(x^{i\gamma_r}\) with eigenvalue just \(\gamma_r\).
We see then an open path. Instead of looking for a strange operator we can use \(D\) (or any of many others that have all real numbers as eigenvalues) and rather modify the space so that it has nothing left but the eigenvalues \(\lambda_r\). But we must see which subspace we choose so that it does not depend on the zeta zeros. Connes-Consani’s procedure is not perfect because \(\mu\) is defined from \(\lambda_r\). But his work gives us an idea that we should look at the space \(E^\perp\) with \(E\) being the set of functions that cancel the Weil quadratic form \(QW(\varphi)=0\).
To learn more
There is a lot of material about Alain Connes on the internet. He has published serious books on mathematics but he also has books talking about mathematics, physics, their relations.
The article we have discussed is posted on arXiv:
A. Connes and C. Consani, Spectral triples and \(\zeta\)-cycles, https://arxiv.org/abs/2106.01715.
And there are several lectures on the internet by Connes explaining this work: North Atlantic Noncommutative Geometry Seminar.
There is another article with Henri Moscovici that is related and we have not commented on. Connes explains it in this conference Conference in honor of Michael Douglas 60th birthday.
There are many interesting lectures by Connes on youtube. Most of them in French, but highly recommended and easy to find. To name a few, Connes was a member of Bourbaki and there is a conference in which several members: Serre, Dixmier, Cartier, talk about their experiences in Bourbaki and which is led by Connes: Bourbaki, les années 1945-75. Otras Le quantique, les mathematiques et le temps}, Alain Connes – “Espace temps, nombres premiers, deux défis pour la géométrie”.
I asked Connes why he uses just the operator \(-ix\frac{d}{dx}\) which he calls the Dirac operator. He refers me to his work: A. Connes, C. Consani,The Scaling Hamiltonian, (2019) arXiv:1910.14368.
To my question of how to construct the appropriate space for the Hilbert-Pólya conjecture, Connes directs me to the work: A. Connes, C. Consani,Hochschild homology, trace map and \(\zeta\)-cycles, arXiv 2207.10419.
Attempts to relate physics to the Riemann hypothesis are abundant and not always successful, a compilation can be found in D. Schumayer, D. A. W. Hutchinson, Physics of the Riemann Hypothesis, arXiv:1101.3116.
The spheroidal prolate functions are especially interesting. There is currently a good reference:
A. Osipov, V. Rokhlin, Hong Xiao, Prolate Spheroidal Wave Functions of Order Zero, Springer, 2013.
The featured image is the Grevillea ‘Moonlight’. The filaments of its flowers are comparable to the zeros of the zeta function in their delicate distribution.


Leave a Reply