As we commented in the post The Triumph of Reason: Newton’s Programme, after the appearance of Newton’s Principia many of the great scientists set out to study natural phenomena armed with the physical principles described by Newton and the most powerful mathematical tool ever invented: the differential and integral calculus, discovered independently by Newton himself and Leibniz (a discovery that also generated one of the most famous controversies in the history of science).
Among the numerous problems related to Newton’s theory of universal gravitation was that of finding the components \(f_{x_1}\), \(f_{x_2}\) and \(f_{x_3}\), of the force of gravitational attraction between non-spherical bodies. Using Newton’s law of gravitation these are given by
$$
f_{x_i}=-G\int \int \int \rho(\xi_1,\xi_2,\xi_3)\frac{x_i-\xi_i}{r^3}\, d\xi_1d\xi_2d\xi_3,\qquad
i=1,2,3,
$$
where \(x_1\), \(x_2\) y \(x_3\) are the Cartesian coordinates in \(\mathbb{R}^3\) and
$$
r=\sqrt{(x_1-\xi_1)^2+(x_2-\xi_2)^2+(x_3-\xi_3)^2}.
$$
One of the earliest attempts to find analytical expressions for the above integrals was by the physicist and mathematician Adrien-Marie Legendre (1752-1833).
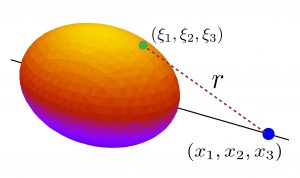
In his case, he was interested in calculating the attraction that a solid of revolution exerts on other bodies, following in the footsteps of McLaurin, d’Alembert and Lagrange. Thus, in an article of 1782 (although published in 1785) entitled Sur l’attraction des sphéroides homogènes, he proved a very interesting theorem which states that, if the value of the force of attraction of a homogeneous (i.e. of constant density) solid of revolution is known at an exterior point situated on its axis, then it is known at any exterior point. Thus he reduced the problem to the study of the radial component \(P(r,\theta,0)\), whose expression is
$$
P(r,\theta,0)=\int \int \int \frac{ (r-r’)\cos{\gamma} }{(r^2-2r r’\cos{\gamma}+r’^2)^{\frac{3}{2}} } r’^2 \sin \theta’ d\theta’,
d\phi’ dr’ \, ,
$$
where \(\cos\gamma=\cos\theta\cos\theta’+\sin\theta \sin \theta’ \cos \phi’\).
In order to solve the problem Legendre developed the function by integrating obtaining the development
$$
\frac{ (r-r’)\cos{\gamma} }{(r^2-2r r’\cos{\gamma}+r’^2)^{\frac{3}{2}}}\!=\!
\frac{1}{r^2} \left\{\! 1\!+\!3 P_2(\cos\gamma)\frac{r’^2}{r^2}\!+\!
5 P_4(\cos\gamma) \frac{r’^4}{r^4}\!+\!\cdots \right\}.
$$
The functions \(P_2, P_4,\dots\) are certain polynomials in the variable \(\cos{\gamma}\), which today are known as Legendre polynomials.
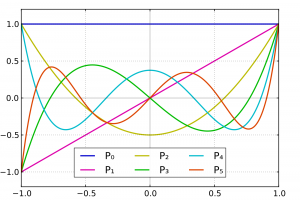
In this same work Legendre finds a general expression that allows to calculate explicitly all the polynomials, some of which can be seen represented in figure 2,
$$
P_n(x)=\frac{(2n-1)!!}{n!}\left[x^n-\frac{n(n-1)}{2(2n-1)}x^{n-2}+
\frac{n(n-1)(n-2)(n-3)}{2\cdot4\cdot(2n-1)(2n-3)}x^{n-4}+\cdots
\right].
$$
Legendre sent his work to the Academy of Sciences and was reviewed, among others, by Laplace, who commented very favourably on it and even expanded it, without, however, even mentioning the young Legendre’s contributions. This very dishonest attitude of Laplace (who tended to ignore many of his fellow mathematicians) contrasted with that of Legendre, who always mentioned his predecessors.
Legendre continued his research and two years later, in 1784, he wrote a second article (published in 1787) in which he deduced several properties of polynomials, including a property of orthogonality:
$$
\int_{0}^{1} P_{2n}(x) P_{2m}(x)dx = \frac{1}{4m+1}\delta_{n,m},
$$
where \(\delta_{m,n}\) is the Kronecker symbol defined by \(\delta_{m,n}=1\) if \(n= m\) and \(0\) otherwise. Using this, Legendre shows that “every” function of the form \(f(x^2)\) is expressed as a series of Legendre polynomials
$$
f(x^2)=\sum_{n=0}^\infty c_n P_{2n}(x),
$$
the coefficients \(c_n\) being univocally determined. The above development is probably the first example of orthogonal development using functions other than sines and cosines, the well-known Fourier series of which we have already spoken here.
In the same paper, Legendre proved that the zeros of \(P_n\) were real, distinct from each other, symmetric about the origin and less than 1 in absolute value. In his fourth paper on the subject (written in 1790, but published three years later) he introduced polynomials of odd degree and proves general orthogonality
$$
\int_{0}^{1} P_{n}(x) P_{m}(x)dx =\frac{2}{2n+1}\delta_{n,m},
$$
as well as the linear differential equation satisfying these polynomials \(P_n(x)\):
$$
(1-x^2) P_n^{\prime\prime}(x)-2x P_n'(x)+n(n+1)P_n(x)=0.
$$
From Legendre’s hands was born the first family of orthogonal polynomials in history, mathematical objects of great utility as would be seen throughout the history of mathematics.
Legendre also introduced the associated Legendre polynomials \(P_n^{m}(x)\) which are expressed through the polynomials \(P_n\) of the form \(P_n^{m}(x)=(1-x^2)^{{m}/{2}} P_n^{(m)}(x)\), where \(P_n^{(m)}(x)\) denotes the \(m\)-th derivative of \(P_n\), and which are solutions of the Laplace equation.
$$
\frac{\partial^2 V}{\partial x^2} + \frac{\partial^2 V}{\partial y^2}+\frac{\partial^2 V}{\partial z^2} =0,
$$
in spherical coordinates after applying the method of separation of variables.
The fact that Legendre’s polynomials were the solution of a differential equation of order two will be the main reason why they appear in the solution of countless problems in physics and mathematics.
As an example of this, we will show how these polynomials allow us to solve a problem very different from the original one solved by Legendre. Specifically, the solution of the Schrödinger equation for the hydrogen atom in spherical coordinates to describe the stationary (time-independent) states of the atom. This equation can be written, for the hydrogen atom, in simplified form as
$$
\left[\Delta_r+\frac1{r^2}\Delta_{\!_\sphericalangle} \right]\Psi(r,\theta,\phi) +[\varepsilon-V(r)]\Psi(r,\theta,\phi)=0,
$$
where the potential is \(V(r)=\alpha/r\) and \(\varepsilon\) represents the values of the electron energy of the hydrogen atom, and
$$
\Delta_r=\frac{1}{r^2}\frac{\partial}{\partial r}\left(r^2\frac{\partial}{\partial r}\right),\quad
\Delta_{\!_\sphericalangle}=\frac1{\sin\theta}\frac{\partial}{\partial \theta}
\left(\sin\theta \frac{\partial}{\partial \theta}\right)+
\frac1{\sin^2\theta}\frac{\partial^2}{\partial \phi^2}
$$
denote the radial and angular Laplacians respectively. Using d’Alembert’s method of separation of variables \(\Psi(r,\theta,\phi)=F(r)Y(\theta,\phi)\) one can obtain the solutions for the radial part \(F(r)\) and the angular part \(Y(\theta,\phi)\). These latter functions turn out to be the spherical harmonics studied by Laplace and which are proportional to the aforementioned associated Legendre polynomials \(P_{l}^{m}\) which in turn are the derivatives of the Legendre polynomials \(P_l\):
$$
Y_{l\,m}(\theta,\phi)= N_{l,m} e^{im\phi} (1-x^2)^{m/2} P_{l}^{m}(x).
$$
Interestingly, these functions determine the shape of the atomic orbitals that many of us heard about in high school chemistry classes. Thus, for \(l=0\) we have one \(s\) orbital (spherical, see figure 3, first line), for \(l=1\) three \(p\) orbitals (see figure 3, second line), \(l=2\) five \(d\) orbitals (see figure 3, third line), etc. A more detailed representation can be seen by clicking here.
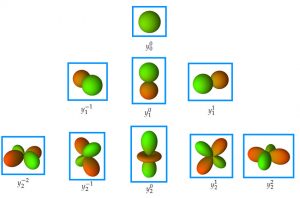
This example shows us that the solution to a concrete problem originating in nature leads to mathematics that goes far beyond its simple use in solving that problem. Indeed, the tools developed by Legendre, Laplace and others to solve the problem of the gravitational attraction of solids of revolution generated mathematical tools capable of solving countless problems in the most diverse areas of science (including mathematics itself). Therein lies part of the magic and beauty of mathematics: once developed, it will always be available to anyone who needs it. This is the universality of mathematics.
For more details on Legendre polynomials you can read the book written by the author available from this link.
For an introduction to quantum mechanics you can download the course Una introducción a la Mecánica Cuántica para “no iniciados”.
The featured image is a collage of the cover page of Legendre’s article and a picture of the hydrogen atom taken with an electron microscope published in PRL 110, 213001 (2013).

Leave a Reply