Isaac Newton stated: “If I have seen further it is by standing on the shoulders of Giants”. Florian and Sergey our heroes today can say the same.
Hypergeometric functions
Latin was a nightmare for me. For two years we had 3 hours of Latin per week. If instead of Caesar with his “little wars” they had put me to translate Gauss on the hypergeometric functions or his masterly Disquisitiones Arithmeticae I would have learned Latin. Years later, with Gauss’s works in my hands, I regretted not having learned anything in those stressful Latin classes. The hypergeometric functions were born in a 23-page work of Gauss written in Latin:
C. F. Gauss, Disquisitiones generales circa seriem infinitam $$ 1+\frac{\alpha\beta}{1\cdot\gamma}x+\frac{\alpha(\alpha+1)\beta(\beta+1)}{1\cdot2\cdot\gamma(\gamma+1)}xx+\frac{\alpha(\alpha+1)(\alpha+2)\beta(\beta+1)(\beta+2)}{1\cdot2\cdot3\cdot\gamma(\gamma+1)(\gamma+2)}x^3+\text{etc.}$$ Commentationes societatis regiae scientiarum Gottingensis recentiores, 2 (1813).
Later Riemann astonished everyone with his surfaces and the synthetic definition of the Gauss function. The Gauss function is determined by having \(0\), \(1\), \(\infty\) as its unique branch points and behaving at them as the powers \(z^\alpha\). The properties of the hypergeometric function follow magically from this definition. Something that deeply annoyed Weierstrass who never approved Riemann surfaces.
After this, there is no branch of mathematics that has not found a subject in hypergeometric functions. The last step is Katz’s Hypergeometric Motives.
We must first generalize. For us a hypergeometric function is one defined by a power series $${}_pF_q\Bigl(\begin{matrix} a_1, &\dots, & a_p\\ b_1, &\dots, & b_q\end{matrix} ; x\Bigr):=\sum_{n=0}^\infty \frac{(a_1)_n\cdots(a_p)_n}{(b_1)_n\cdots(b_q)_n}\cdot \frac{x^n}{n!},$$ where \((a)_n:= a(a+1)\cdots(a+n-1)\).
The giants came first
Already Gauss noticed that in some cases his function was algebraic. For example Gauss writes $$(t+u)^n+(t-u)^n=2t^n{}_2F_1(-\tfrac{n}{2},\tfrac{1-n}{2};\tfrac12; \tfrac{u^2}{t^2}),$$ that is, $${}_2F_1(-\tfrac{n}{2},\tfrac{1-n}{2};\tfrac12; x)=\frac{(1+\sqrt{x})^n+(1-\sqrt{x})^n}{2}.$$ Herman Schwarz in 1873 solved the problem of when the Gauss function \({}_2F_1([\alpha,\beta],[\gamma],x)\) is an algebraic function of \(x\). A power series \(f(x)=\sum_{n=0}^\infty a_n x^n\) is said algebraic if there is a polynomial in two variables \(p(x,y)\in\mathbb C[x,y]\) such that \(p(x,f(x))=0\) in the ring of power series \(\mathbb C[[x]]\).
Schwarz was a mathematician who liked concrete problems, obtaining the solution by techniques that others later generalized. It is in this work that he constructs the modular function by the conformal transformation of a triangle with arc sides into a half-plane. To each hypergeometric function Schwarz associates a triple of numbers \((\lambda,\mu,\nu)=(1-\gamma,\gamma-\alpha-\beta,\alpha-\beta)\) and gives a list of triples of numbers, such that \({}_2F_1([\alpha,\beta], [\gamma],x)\) is algebraic (assuming that \(\lambda\), \(\mu\), \(\nu\in \mathbb Q \smallsetminus\mathbb Z\)) if and only if \((\lambda,\mu,\nu)\) or some permutation, sign change, or some sum with a triple of integers with even sum, appears in the list.

Apart from being a mathematician, Schwarz was the head of the Volunteer Fire Brigade and assisted the stationmaster in opening and closing the train doors.
We already have three giants, Gauss, Riemann and Schwarz, the next giant is Gotthold Eisenstein who developed a theorem about power series defining algebraic functions, which was later refined by Heinrich Eduard Heine.
Theorem (Eisenstein 1852, Heine 1853). If a power series \(f(x)\in \mathbb Q[[x]]\) is an algebraic function, then there exists a nonzero integer \(M\) such that \(f(Mx)-f(0)\in \mathbb Z[[x]]\).
In particular the coefficients of a rational power series that is an algebraic function contain only a finite number of primes in its denominators.
We will say that a power series \(f\) is almost integral if it satisfies Eisenstein’s criterion.
Edmund Landau in 1904 and 1911 uses Eisenstein’s theorem to obtain a necessary condition for the Gauss hypergeometric function to be algebraic.
Theorem (Landau) Let \(F(x)={}_2F_1(\alpha,\beta;\gamma;x)\) such that \(\alpha\), \(\beta\), \(\gamma\), \(\alpha-\gamma\) and \(\beta-\gamma\) are rational but not integers. Let \(N\) be the common denominator of the numbers \(\alpha\), \(\beta\) and \(\gamma\). Then \(F\) satisfies Eisenstein’s condition if and only if for every \(\lambda\) relatively prime with \(N\) and such that \(1\le \lambda\le N\), we have $$\langle \lambda \alpha\rangle<\langle \lambda \gamma\rangle<\langle \lambda \beta\rangle \quad \text{or}\quad \langle \lambda \beta\rangle<\langle \lambda \gamma\rangle<\langle \lambda \alpha\rangle,$$ where \(\langle x\rangle\) denotes the fractional part of \(x\).
Alfred Errera proved in 1913 that the Landau condition is equivalent to the Schwarz classification. That is, the Landau condition is also sufficient for the Gaussian function to be algebraic.
The case of generalized hypergeometric functions
Gauss and Schwarz, Eisenstein and Heine, and Landau, Errera completed the study of when the Gauss hypergeometric function is algebraic. New mathematicians took up the subject for generalized hypergeometric functions.
The case of generalized hypergeometric functions was considered by Gilles Christol in 1986, who managed to extend Landau’s results. Shortly after, the problem was completely solved by Frits Beukers and Gert Heckman for $${}_pF_q([a_1,\dots,a_p]; [b_1,\dots b_q];x)$$ when the coefficients \(a_j\), \(b_k\in \mathbb Q\) are rational for all \(j\), \(k\) and \(a_j\), \(a_j-b_k\notin \mathbb Z\).
The criterion refers to a power series $$F(x)={}_pF_{p-1}\Bigl(\begin{matrix} a_1, &\dots, & a_p\\ b_1, &\dots, & b_{p-1}\end{matrix} ; x\Bigr)$$ with \(a_1\), . . . , \(a_p\), \(b_1\), . . ., \(b_{p-1}\in \mathbb Q\smallsetminus (-\mathbb N)\) and says the following.
Theorem (Christol, Beukers, Heckman, Katz). Let \(F(x)\) be the function shown above. Suppose \(a_j\), \(a_j-b_k\notin\mathbb Z\) for all \(j\), \(k\). Let \(N\) be the least common denominator of the parameters. Then \(F\) is algebraic if and only if the numbers \(A=\{e^{2\pi i\lambda a_1},\dots, e^{2\pi i \lambda a_p}\}\) and the \(B=\{e^{2\pi i \lambda b_1},\dots, e^{2\pi i\lambda b_{p-1}}, e^{2\pi i \lambda}\}\) alternate on the unit circle for all \(1\le \lambda\le N\) with \(\mathop{\rm gcd}(\lambda,N)=1\).
With these results the problem is essentially solved. The solution is comparable to a Greek sculpture or a Beethoven sonata. The hypergeometric functions extend to the entire complex plane except for three singularities \(0\), \(1\), \(\infty\).
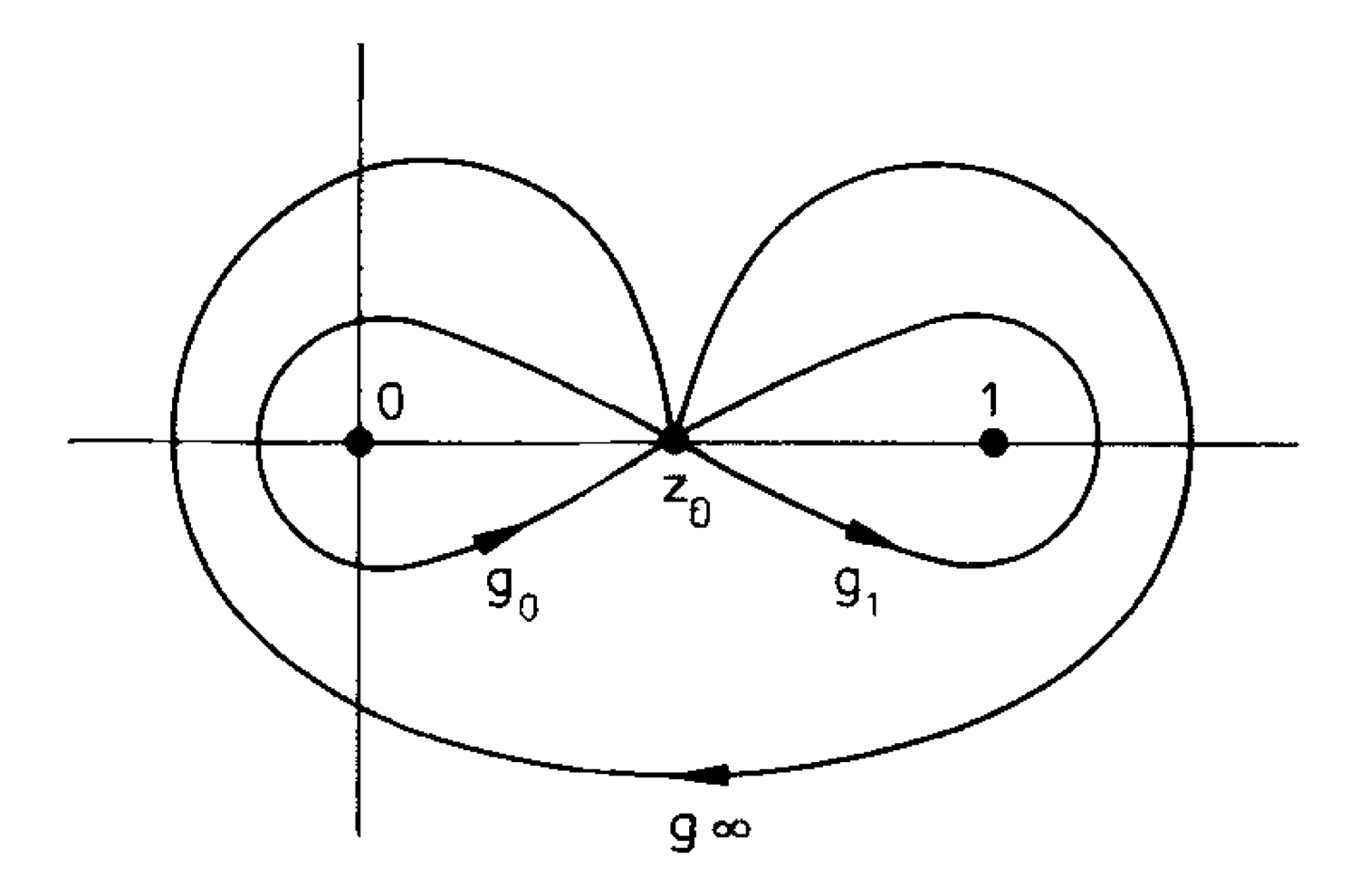
Riemann already understood that the fundamental piece is the monodromy group. Every closed curve that starts at a regular point \(z_0\) and returns to it without passing through singularities interchanges the various branches of the hypergeometric function. This determines a group. The essential part of the solution is contained in the work of Frits Beukers and Gert Heckman and consists in determining exactly the monodromy group of the function \({}_nF_{n-1}(x)\) as a function of the parameters. The function is algebraic if and only if the group is finite. These finite groups generated by reflections on \(\mathbb C^n\) were already determined. It turns out that these cases of algebraic functions are like accidents, resulting essentially in a finite number of cases in each dimension \(n\). Functions with incredible symmetry, similar to regular polyhedra in each dimension.
The remaining problem
And we come to the object of our entry today. As Florian Fürnsinn and Sergey Yurkevich observe, the assumptions on the rationality of the parameters made in the criterion of Beukers-Heckman are not justified, they give the example $${}_3F_2\Bigl(\begin{matrix} 1/2& \sqrt{2}+1& -\sqrt{2}+1\\ \sqrt{2} & -\sqrt{2} &\end{matrix}; 4x\Bigr)=\frac{(7x-1)(2x-1)}{(1-4x)^{5/2}}=1+x-6x^2+\cdots\in\mathbb Z[[x]],$$ whose parameters are not rational while the function is actually algebraic. Also the function $${}_2F_1\Bigl(\begin{matrix} 2 & 2\\ 1& \end{matrix}; x\Bigr)=\frac{(1+x)}{(1-x)^3},$$ is algebraic, but the Beukers-Heckman criterion does not apply since there are integer differences between its parameters.
Florian and Sergey provide an algorithm that decides whether a hypergeometric function is algebraic or not, whatever its parameters are.
To talk about its algorithm it is convenient to consider power series $$\mathcal F(x)=\mathcal F\Bigl(\begin{matrix} a_1, &\dots, & a_r\\ b_1, &\dots, & b_s\end{matrix} ; x\Bigr)=\sum_{n=0}^\infty \frac{(a_1)_n\cdots (a_r)_n}{(b_1)_n\cdots (b_s)_n}x^n$$ The hypergeometric function differs in that one of the \(b_j=1\).
We say that \(\mathcal F\) is reduced if for every pair \((j,k)\), we have \(a_j-b_k\notin\mathbb Z\). And we say that \(\mathcal F\) is contracted if \(a_j-b_k\notin\mathbb N\).
To each function \(\mathcal F\) we associate its contraction \(\mathcal F^c\). This is obtained, taking from all the differences \(a_j-b_k\in \mathbb N\) one with minimum value \(a_{j_0}-b_{k_0}\) and eliminating this pair of indexes. Repeating this operation until we obtain a \(\mathcal F^c\) that is contracted. For example, in the previous case $${}_3F_2\Bigl(\begin{matrix} 1/2& \sqrt{2}+1& -\sqrt{2}+1\\ \sqrt{2} & -\sqrt{2} &\end{matrix}; x\Bigr)=\mathcal F\Bigl(\begin{matrix} 1/2& \sqrt{2}+1& -\sqrt{2}+1\\ \sqrt{2} & -\sqrt{2} &1\end{matrix}; x\Bigr)$$ successively transforms into $$\mathcal F\Bigl(\begin{matrix} 1/2& \sqrt{2}+1\\ \sqrt{2} &1\end{matrix}; x\Bigr)$$ $$ \mathcal F\Bigl(\begin{matrix} 1/2& & \\ 1\end{matrix}; x\Bigr)={}_1F_0\Bigl(\begin{matrix} 1/2&\\ \{\}\end{matrix}; x\Bigr)=(1-x)^{-1/2}.$$
Another example $${}_2F_1\Bigl(\begin{matrix} 1/2 & 2\\ 3/2 & \end{matrix};x\Bigr)=\mathcal F \Bigl(\begin{matrix} 1/2 & 2\\ 3/2 & 1\end{matrix};x\Bigr)\to\mathcal F \Bigl(\begin{matrix} 1/2 \\ 3/2\end{matrix};x\Bigr)={}_2F_1\Bigl(\begin{matrix} 1/2 & 1 \\ 3/2& \end{matrix};x\Bigr)$$ which is contracted but not reduced.
Florian and Sergey’s basic result is that \(\mathcal F\) is algebraic if and only if its contraction is algebraic. With these elements we can describe their algorithm
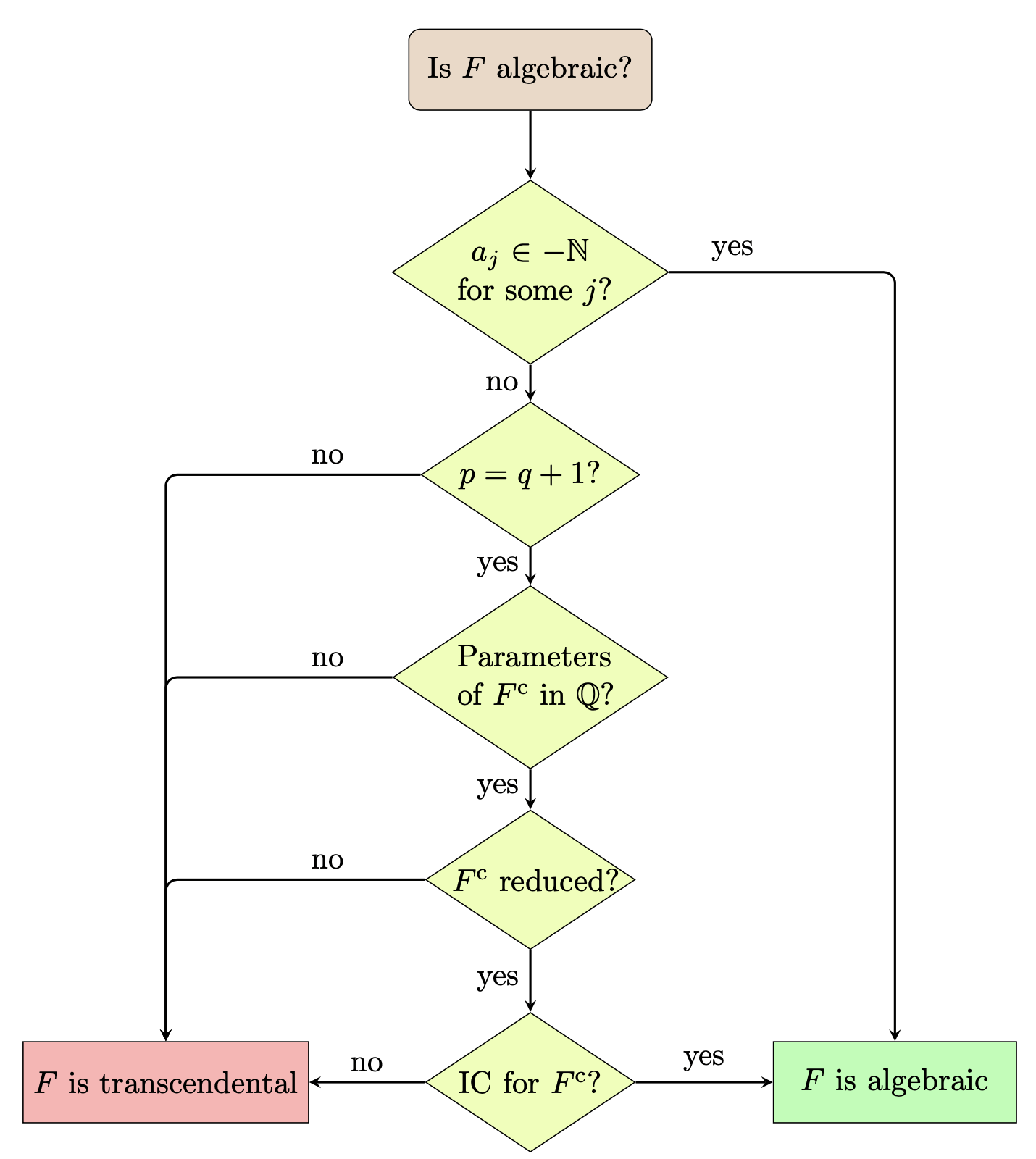
If any of the \(a_j\in -\mathbb N\) the function is a polynomial. A hypergeometric function \({}_pF_q(x)\) can only be algebraic if \(p=q+1\). A contracted and algebraic function must have rational parameters and be reduced. Finally, for a function that has reached this point it is algebraic if and only if it satisfies the Beukers-Heckman unit root alternation criterion.
Florian} is a Ph.D. student at the University of Vienna and Sergey is a PostDoc at the same university. They have both worked on their thesis with Professor Herwig Hauser, whose website is worth a visit. I wouldn’t miss his Gallery of singularities, that I have got to know through this entry.


Ira Gessel and his excursions
Ira Gessel is a mathematician working in combinatorics. In 2001 he considered the problem of excursions in the first quadrant \(Q:=\{(x,y)\colon x, y\ge 0\}\), starting at the origin and ending at the origin with steps \(i\), \(-i\), \(1+i\) and \(-1-i\). Note that these steps are not allowed if they take us outside \(Q\). Gessel observed that the number of walks of length \(m\) is zero if \(m\) is odd and when \(m=2n\) is even, then this number is $$g_{2n}=16^n \frac{(5/6)_n(1/2)_n}{(5/3)_n(2)_n},\qquad n\ge0.$$ But this was merely an observation. This conjecture is equivalent to saying that $$\sum_{n=0}^\infty g_n x^n= {}_3F_2\Bigl(\begin{matrix}5/6 & 1/2 & 1\\5/3 & 2 & \end{matrix}; 16x^2\Bigr).$$ Manuel Kauers, Christoph Koutschan and Doron Zeilberger proved the conjecture in 2008 with the help of computers. They find a recurrence for \(g_n\), the recurrence expresses \(g_{n+32}\) in terms of \(g_{n+j}\) with \(0\le j<32\) and coefficients that are polynomials in \(n\) of degree 172, and polynomials where 385-digit integers are involved. The proof consists then in seeing that the formula imagined by Gessel satisfies this recurrence and that the first 32 values coincide. This work was published in the prestigious Proceedings of the National Academy of Science, USA.
In 2015 Alin Bostan, Irina Kurkova and Kilian Raschel published their paper A human proof of Gessel’s lattice path conjecture.
Well, the function \(\sum_{n=0}^\infty g_nx^n\) is algebraic, but this was not observed until 2010. The Beukers and Heckman criterion does not apply directly since there are integer differences between their parameters. Which makes Florian and Sergey’s work interesting. There will be no more undetected algebraic hypergeometric functions.
Speaking of Ira Gessel, we cannot fail to mention his role in the free right to certain physiological needs. See also.
End
Florian and Sergey knew the example of Gessel walks and others where the Beukers-Heckman criterion did not apply. Working on these topics on power series and their algebraicity it was natural for them to come up with the problem.
“We relatively quickly found out, how our criterion should look like and also had the main ideas quickly gathered. However, the precise arguments we found for some assertions were more technical and tedious than anticipated, but all in all we really enjoyed the work. We were both sharing an office at that time, and it was a very nice experience having a common project.”
Learn more
The paper we celebrate today can be found in arXiv. It is not difficult to read, although it naturally uses the results of previous articles.
Particularly interesting is undoubtedly
that we can download from some sites on the web.
Also Schwartz’s article is freely available on the web. The difficulty of German is now lighter with current translation methods.
Hermann Amandus Schwarz, Ueber diejenigen Fälle, in welchen die Gaussische hypergeometrische Reihe eine algebraische Function ihres vierten Elementes darstellt, J. Reine Angew. Math. 75 (1873), 292-335. [Beware! This download the entire volume of the journal]
How the subject has evolved from Gauss to the theory of motives can be seen in the article by Rodríguez Villegas in the Notices of the American Mathematical Society.
The featured image today are flowers in a pond, the symmetry of these flowers resemble the symmetries that represent the algebraic hypergeometric functions.


Leave a Reply