Not all problems are the same. Some are hard to understand, like the Hodge conjecture, for whose solution they offer a \(1,000,000\$\) prize, but they might as well give \(100,000\$\) for understanding it. Others are easy to understand but almost impossible to solve, such as Goldbach’s conjecture: is every even number the sum of two primes? Others like the one we present today is not difficult to understand and it has just been proposed. Its difficulty remains to be seen, it may be easy, since it has not yet been attempted by many mathematicians.
Problem posing is a very complicated task. Anyone can pose inaccessible or trivial problems. But getting a problem that is easy to understand, not trivial, but that does not seem impossible to solve is a difficult art. The one we present today has all the ingredients to make it a great problem. That’s why I think its authors deserve recognition. The problem has for those who need it (which is not my case) the attractive of having been proposed by non-mathematicians because of its possible applications.
The problem concerns a finite family of finite sets. Before stating it we need to understand the inclusion-exclusion principle.
Inclusion-exclusion Principle
The typical Venn diagram consists of three sets \(A\), \(B\) and \(C\) showing their intersections
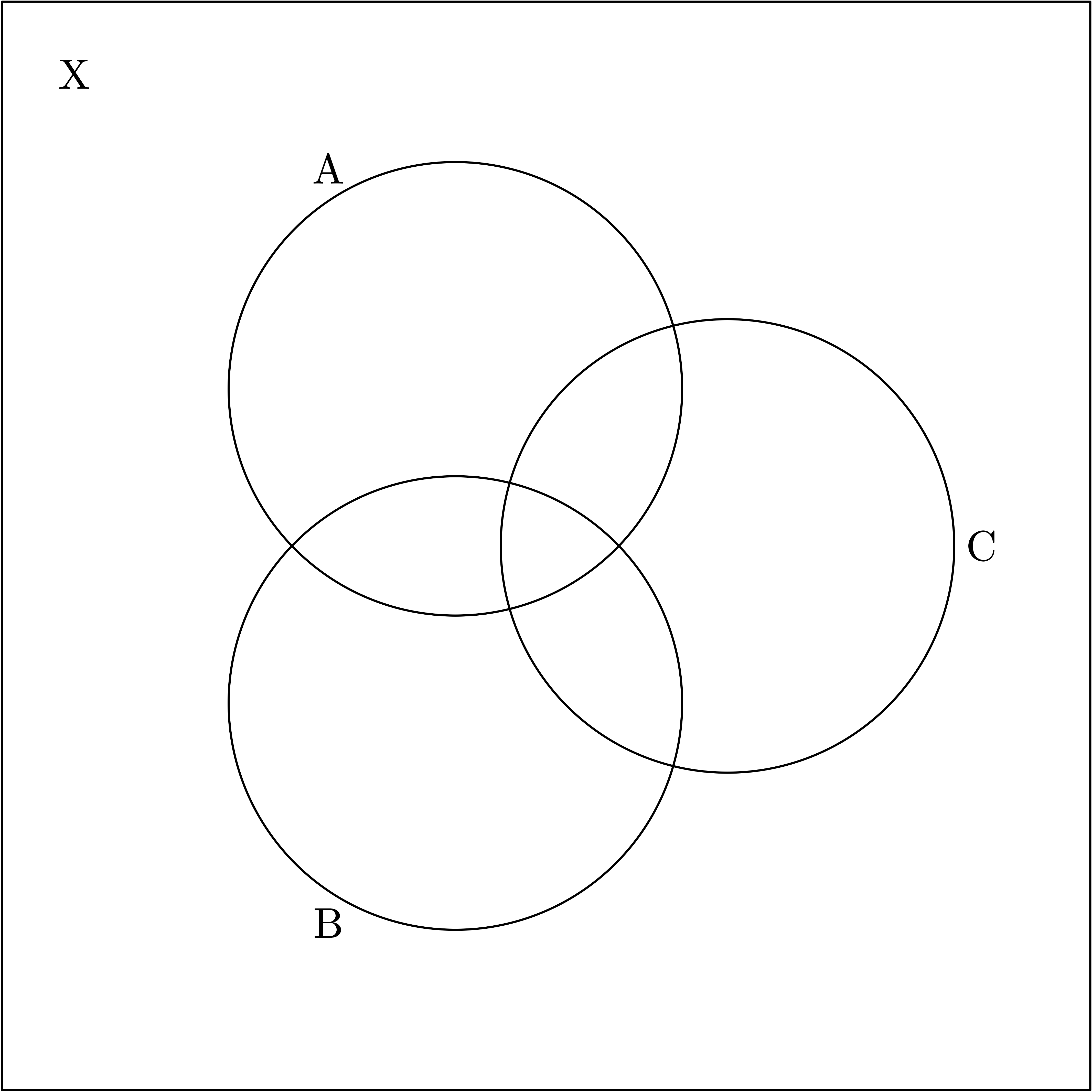
We can use it to count the elements of the complement of the union \(X\smallsetminus A\cup B\cup C\). If we denote by \(|A|\) the cardinal of the finite set \(A\), we will have \begin{align*}
|X\smallsetminus &(A\cup B\cup C)|\\
&=|X|-|A|-|B|-|C|\\
&+|A\cap B|+|A\cap C|+|B\cap C|\\&-|A\cap B\cap C|.
\end{align*} This can be generalized to the case of a finite number of sets \(A_1\), \(A_2\), . . . , \(A_N\). For the general case it is convenient to introduce some notation. Let \(I=\{1,2,\dots, N\}\) be the set of subscripts and \(J\subset I\) be a subset, we can define the intersection $$A_J:=\bigcap_{j\in J} A_j,\qquad A_\emptyset:=X.$$ When \(J=\emptyset\) the definition we give is coherent/convenient if a bit artificial. Then the principle is stated, using \(|A|\) to denote the cardinal of a set $$\Bigl|X\smallsetminus\bigcup_{j=1}^N A_j\Bigr|=\sum_{J\subset I} (-1)^{|J|}|A_J|.$$
The exclusion-inclusion principle is even more general. I take this opportunity to introduce a notation, due to Iverson but promoted by Donald Knuth, which is very convenient. If \(P\) is a proposition we denote by \([ P]\) the number \(1\) if \(P\) is true and \(0\) if it is false. Thus \([ x\in A]\) is the characteristic function of the set \(A\). This notation is especially convenient when we apply Fubini’s theorem. For example we convert the integral on a flat domain \(D\) into the integral on a rectangle by introducing a factor \([ P(x,y)\le 0]\) into the integrand. Clearing the unknown \(x\) or \(y\) we obtain the limits of integration. For example $$[ x^2+y^2 \le1] =\Bigl [ -\sqrt{1-y^2}\le x\le \sqrt{1-y^2}\Bigr ].$$
The general exclusion-inclusion principle can then be written as follows $$\Bigl [ x\in X\smallsetminus\bigcup_{j\in J} A_j\Bigr]=\sum_{J\subset I}(-1)^{|J|} [ x\in A_J].$$ We still need to simplify the above expression a bit.
Let’s suppose now that \(X=\bigcup_{j=1}^N A_j\), in this case the exclusion-inclusion principle tells us that $$0=\sum_{J\subset I}(-1)^{|J|} [ x\in A_J].$$ Taking into account that one of the terms of this sum is \(A_\emptyset = X=\bigcup_{j=1}^N A_j\) we obtain that $$\Bigl [ x\in \bigcup_{j=1}^N A_j\Bigr]=-\sum_{J\ne\emptyset}(-1)^{|J|} [ x\in A_J]\qquad \qquad(1).$$ The union of the sets \(A_j\) can be expressed in terms of the intersections \(A_J\).
But in general there are empty intersections, or it can also happen that for \(J_1\ne J_2\) one has \(A_{J_1}=A_{J_2}\). Let \(B_1\), \(B_2\), . . . , \(B_M\) be the distinct intersections between \(A_J\) with \(J\ne\emptyset\). We can regroup the terms in (1) and we get $$\Bigl [ x\in \bigcup_{j=1}^N A_j\Bigr]=\sum_{m=1}^K a_m [ x\in B_m]\qquad \qquad(2),$$ where the coefficients \(a_m=-\sum_{A_J=B_m}(-1)^{|J|}\) are positive or negative integers and nonzero (if \(a_m=0\) for some \(m\) we can eliminate that term from the sum). Equation (2) is what we will call the canonical expression of the inclusion-exclusion for the \(A_j\).
The Conjecture
Let \(A_1\), . . . , \(A_N\) be finite sets. Let \(B_1\), . . . , \(B_K\) be the intersections of these sets appearing in the canonical expression (2). The conjecture states that we can construct the union \(\bigcup_{n=1}^N A_n\) from the sets \(B_m\) using the two operations union and complement with the restriction that the unions apply to disjoint sets and the complements are only used to express differences \(C_1\smallsetminus C_2\) satisfying \(C_2\subset C_1\).
That is, the conjecture asserts that there exists a sequence \(C_1\), . . . , \(C_R\) of sets such that \(C_R= \bigcup_{n=1}^N A_n\), and for each \(C_r\) in the sequence, one of the following conditions is satisfied
- (a) \(C_r=B_m\) for a certain value \(1\le m\le K\).
- (b) \(C_r=C_s\cup C_t\) with \(s\), \(t<r\) and \(C_s\cap C_t=\emptyset\).
- (c) \(C_r=C_s\smallsetminus C_t\) with \(s\), \(t<r\) and \(C_t\subset C_s\).
Let us consider an example. We give the initial sets \begin{gather*}A_1=\{3,4,5,7\},\quad A_2=\{1,2,7,10\}\\A_3=\{1,4,5,8\},\quad A_4=\{2,4,8,9\},\\ A_5=\{1,5,7,9\},\quad A_6=\{1,3,6,7\},\\ A_7=\{1,2,4,9\}\end{gather*} The canonical expression is complicated here. What we will do is to give the list of sets with positive coefficient in the form \(B_1^r\), \(B_2^s\), . . . where the exponents are the coefficients \(a_m\) in the canonical expression. We will not write the exponent \(1\). The terms with positive coefficients are \(\{1\}^2\), \(\{4\}\), \(\{5\}\), \(\{7\}\), \(\{1,2,4,9\}\), \(\{1,2,7,10\}\), \(\{1,3,6,7\}\), \(\{1,4,5,8\}\), \(\{1,5,7,9\}\), \(\{2,4,8,9\}\), \(\{3,4,5,7\}\).
The terms with negative coefficients are \(\{1,2\}^{-1}\), \(\{1,4\}^{-1}\),\(\{1,5\}^{-1}\), \(\{1,7\}^{-2}\), \(\{1,9\}^{-1}\), \(\{3,7\}^{-1}\), \(\{4,5\}^{-1}\), \(\{4,8\}^{-1}\), \(\{5,7\}^{-1}\), \(\{2,4,9\}^{-1}\).
We can reconstruct the union using these sets, e.g. as \begin{align*}&\{1,2,4,9\}\cup(\{2,4,8,9\}\smallsetminus\{2,4,9\})\cup\\&\cup\{5\}\cup(\{1,2,7,10\}\smallsetminus\{1,2\})\cup\\&\cup (\{1,3,6,7\}\smallsetminus\{1,7\})\end{align*}
Some intersections appear with coefficient \(0\). Using those sets to reconstruct \(X\) is forbidden and intuitively should be unnecessary given equation (2). In this case there are few: \(\emptyset\), \(\{2\}\) and \(\{9\}\).
Versions of the Conjecture
The sum of two characteristic functions \([ x\in A]+ [ x\in B]\) is a characteristic function \([ x\in A\cup B]\) if and only if \(A\) and \(B\) are disjoint. The difference \([ x\in A]- [ x\in B]\) is a characteristic function \([ x\in A\smallsetminus B]\) if and only if \(B\subset A\). In the previous example the conjecture told us that we could express the union \(\{1,2,\dots, 10\}\) in the form \begin{align*}&\{1,2,4,9\}\cup(\{2,4,8,9\}\smallsetminus\{2,4,9\})\cup\\&\cup\{5\}\cup(\{1,2,7,10\}\smallsetminus\{1,2\})\cup\\&\cup (\{1,3,6,7\}\smallsetminus\{1,7\})\end{align*} and this is equivalent to \begin{align*}
[ x&\in \{1,2,\dots, 10\}]= [ x\in \{1,2,4,9\}]\\&+( [ x\in \{2,4,8,9\}]- [ x\in \{2,4,9\}])\\&\mskip-30mu+ [ x\in \{5\}]+( [ x\in \{1,2,7,10\}]- [ x\in \{1,2\}])\\&+( [ x\in \{1,3,6,7\}]- [ x\in \{1,7\}])\end{align*} where each parenthesis (even those that are not explicitly placed corresponding to the sums) is a function that only takes the values \(0\) and \(1\), that is to say, it is a characteristic function. In general the conjecture is equivalent to saying that there exists an expression of the characteristic function of the union \(\bigcup A_n\) by sums and differences of the characteristic functions of the sets \(B_m\) appearing in the canonical expression, with an order in the operations expressed by means of parentheses, and such that each parenthesis is a characteristic function.
When in this expression we simplify and group the equal terms, we obtain an expression $$\Bigl\lbrack x\in \bigcup_{j=1}^N A_j\Bigr\rbrack=\sum_{m=1}^K c_m\lbrack x\in B_m\rbrack,$$ where now the \(c_m\) could be \(=0\), if some of the intersections have not been used.
Strong Conjecture. We can express the characteristic function of the union of the sets \(A_m\), in the above form, i.e., with the parentheses always equal to characteristic functions and such that \(|c_m|\le |b_m|\) and with equals signs, i.e., \(c_m b_m\ge0\).
It also seems to be true, though less interesting, that there is such an expression with \(c_m=b_m\). But actually the smaller \(\sum_{m=1}^K|c_m|\) the better the expression looks.
The Authors
Antoine Amarilli is an associate professor in the DIG team of the Télécom Paris engineering school in France, and apart from his interest in Computer Science he is very involved in the climate crisis, he also maintains a blog. Mikaël Monet, is a full-time researcher in computer science at Inria Lille, and Dan Suciu is a Microsoft Endowed Professor in Computer Science and Engineering at the University of Washington.



They have formulated the conjecture as a consequence of their work that have to do with probabilistic databases, i.e. in which the answer to a question is not univocal but has certain probabilities. The problem has to do with the strategy followed to use these databases and the existence of certain circuits for their implementation. Their merit consists in having formulated a precise mathematical question. They have also confirmed the conjecture in the simplest cases, all those in which the total set has \(\le5\) elements. The \(5\) may seem small but we are considering \(2^{2^5}\) possibilities, which can be reduced if we take into account isomorphisms. They have also checked many cases with more elements.
I have done randomized experiments myself, the example I have shown is one of them. Given the initial family of sets \((A_n)\) I have built a program that gives me the corresponding canonical representation. From it I have searched by hand for a way to express the total set \(X\) using the allowed sets, with the appropriate sign. A sort of sudoku, of which I sometimes doubted whether I could manage to express \(X\). But I always had the surprise of getting it after several attempts. It seemed like magic.
It is possible to prove that if we were to use all the \(A_J\) interceptions and not only those with a non-zero \(a_m\)-coefficient, then we can obtain \(X\) using only disjoint unions and differences \(C_1\smallsetminus C_2\) with \(C_2\subset C_1\). But for the practical applications we need to use only the intersections with coefficients \(a_m\ne0\).
Learn More
The paper we are discussing today contains the formulation of the conjecture and unsuccessful attempts to test it. It appeared in arXiv in January of this year.
The Mathematica program that I have used to obtain the canonical expression is

The program prints “Mobius”, which is a list with elements of type \(\{\{4,8\},-1\}\) containing a set \(B_m\) and its coefficient \(a_m\).
Consider the case of three sets with all intersections non empty
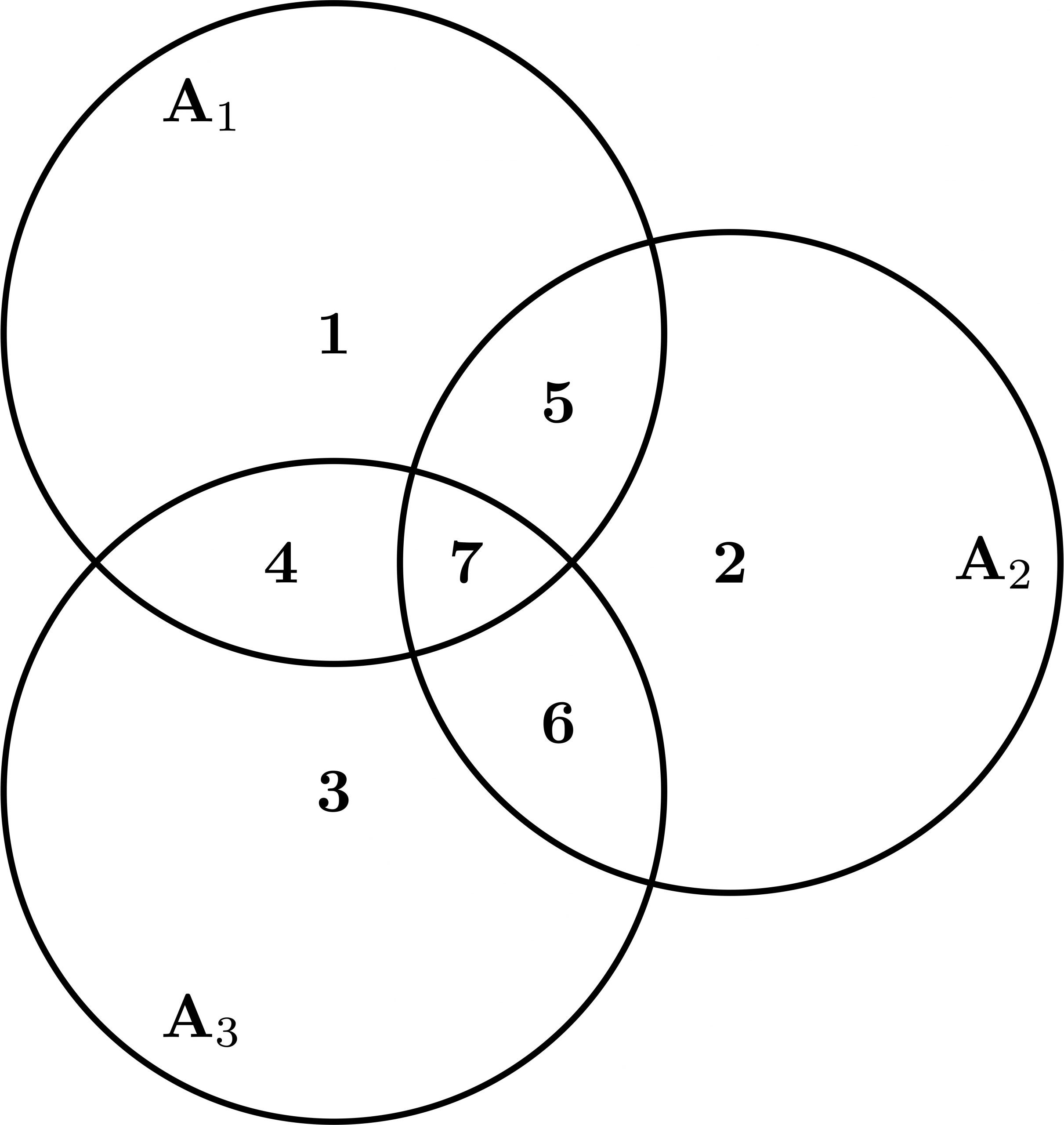
In this case, the intersections are \(B_1=\{1,4,5,7\}\), \(B_2=\{2,5,6,7\}\), \(B_3=\{3,4,6,7\}\), \(B_4=\{5,7\}^{-1}\), \(B_5=\{4,7\}^{-1}\), \(B_6=\{6,7\}^{-1}\) and \(B_7=\{7\}\). We can obtain the union, by means of the allowed operations, using all the intersections and with the appropriate sign. For example \begin{align*} &A_1\cup A_2\cup A_3\\&=B_1\cup(B_2\smallsetminus B_4)\cup\bigl[(B_3\smallsetminus B_5)\smallsetminus(B_6\smallsetminus B_7)\bigr]\end{align*} note that \(B_7\) carries two \(-\) signs, so it counts as adding once. Such a decomposition exists in general with \(N\) sets with all nonempty intersections.
The above representation with \(N=3\) sets is valid for the case of 3 sets in any case. Even if some of the intersections are empty. For example removing the element \(4\) in all the previous sets we will have \(B_5=A_1\cap A_3=A_1\cap A_2\cap A_3=B_7\). Therefore this intersection goes with coefficient \(=0\) and cannot be used. We used it twice in the previous representation, once with positive sign and once with negative sign. The solution here would be simple, it is enough to substitute in the above representation \(\bigl[(B_3\smallsetminus B_5)\smallsetminus(B_6\smallsetminus B_7)\bigr]\) by \(B_3\smallsetminus B_6\) which is allowed since the \(4\) is not now contained in \(B_1\). But all this in the general case, of \(N\) sets, is too messy.
I have used the notation \([P]\) frequently since I read Knuth’s paper
Donald Knuth, Two notes on notation, Amer. Math. Monthly 99 (1992) 403-422. arXiv:math/9205211.
In many cases, such as using Fubini’s theorem, it can greatly clarify ideas.
The featured image today is from the user herraez.

Leave a Reply