Este año 2017 se cumplen 100 años del nacimiento de Edward N. Lorenz, matemático y meteorólogo estadounidense, una figura clave en el nacimiento de la teoría del caos.
Lorenz estudió matemáticas en el Dartmouth College de New Hampshire y en la Harvard University en Cambridge, y desde 1942 a 1946 estuvo en la fuerza aérea de los Estados Unidos, trabajando como meteorólogo. Al final de la Segunda Guerra Mundial estudió Meteorología y se doctoró en el Massachusetts Institute of Technology, donde trabajaría de profesor hasta su jubilación.
En 1963 publicó su legendario artículo «Deterministic Nonperiodic Flow» en el Journal of the Atmospheric Sciences, en el que mostraba cómo pequeñas perturbaciones en los datos iniciales de un sistema podían producir, con el tiempo, enormes efectos.
Lorenz se preguntaba por qué, si se conocían las ecuaciones y las condiciones iniciales, no se conseguía predecir el tiempo atmosférico que iba a hacer dentro de tres días con una fiabilidad aceptable. Para tratar de entender lo que pasaba, simplificó al máximo las ecuaciones de la circulación atmosférica terrestre (las podemos ver en [1]), y planteó el siguiente sistema dinámico determinista tridimensional no lineal que ahora lleva su nombre:
\(\left\{ \begin{array}{l} \displaystyle\frac{dx}{dt} = \sigma (y-x), \\ \displaystyle\frac{dy}{dt} = (\rho-z)x – y,\\ \displaystyle\frac{dz}{dt} = xy – \beta z, \end{array} \right.\)
donde \(\sigma\), \(\beta\) y \(\rho\) son tres parámetros positivos a los que asignó los valores \(\sigma=10\), \(\beta=8/3\) y \(\rho=28\). Simplificado hasta este punto, el sistema ya no tiene ninguna utilidad para hacer previsiones meteorológicas; sin embargo, posee los ingredientes necesarios para ser representativo de los movimientos atmosféricos y constituye el modelo teórico de caos determinista más célebre y más estudiado.
A pesar de su aspecto relativamente sencillo, el sistema anterior no tiene solución analítica, así que Lorenz se puso a resolverlo con métodos numéricos y la ayuda de un ordenador. Casi por casualidad, al repetir unos cálculos introduciendo valores anteriormente obtenidos pero con un levísimo redondeo (tomando solo tres valores decimales para escribir menos) observó, con gran sorpresa, cambios drásticos en los resultados (los detalles de la historia se pueden consultar en [2]). Así, pudo concluir lo siguiente:
- La evolución de cada una de las componentes \(x(t)\), \(y(t)\) y \(z(t)\) de la solución tiene un comportamiento aparentemente azaroso.
- Si, en el espacio \(xyz\), dibujamos la sucesión de valores que en el transcurso del tiempo toman las soluciones, se obtiene una trayectoria que se enrolla sobre un curioso objeto de dos lóbulos (se observa claramente en la figura adjunta). Era el primer ejemplo de lo que ahora se denomina «atractor extraño».
- La introducción de un pequeñísimo error en los datos iniciales crece exponencialmente con el cálculo, de forma que, al cabo de un tiempo relativamente pequeño, se obtiene un resultado radicalmente diferente. Esto pone en evidencia la sensibilidad del sistema respecto de las condiciones iniciales.
En la figura, con los mismos parámetros \(\sigma\), \(\beta\) y \(\rho\) que usó Lorenz, y partiendo de las condiciones iniciales \(x(0)=y(0)=z(0)=1\), mostramos la trayectoria en el espacio que describe la curva \((x(t), y(t), z(t))\) cuando \(t\) varía entre \(1\) y \(30\) (prescindimos de lo que ocurre con \(t\) entre \(0\) y \(1\) para esperar a que la trayectoria «entre» en el atractor y que este se vea mejor).
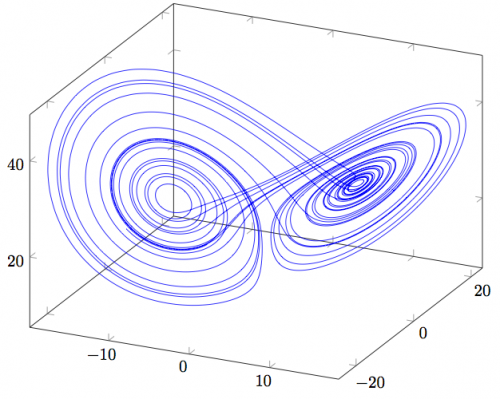
Curva \((x(t), \, y(t), \, z(t))\) solución de la ecuación de Lorenz.
Si el modelo muy simplificado de Lorenz ofrece un comportamiento tan caótico, no cabe esperar que el comportamiento de las verdaderas ecuaciones que rigen el tiempo atmosférico \(—\)mucho más complicadas, por supuesto\(—\) sea más predecible. Si alguien te dice qué tiempo va a hacer en tu ciudad dentro de un mes, no te lo creas. Eso sí, si es verano, tenderá a hacer calor; y, si es invierno, posiblemente hará frío.
Años más tarde, Lorenz también introdujo el concepto de «efecto mariposa», popularizado de muchas maneras; por ejemplo, con la frase «el aleteo de una mariposa en Brasil puede ocasionar un tornado en Texas». Con él quería explicar el comportamiento caótico de sistemas inestables, tales como el tiempo meteorológico, en los que un pequeño cambio en las condiciones iniciales \(—\)y, en la práctica, tales condiciones son imposibles de conocer con total exactitud\(—\) se magnifica de manera descomunal según va avanzando el tiempo. Eso sí, que el atractor de Lorenz se parezca a las alas de una mariposa es pura coincidencia.
Referencias
[1] M. Lezaun, Predicciones del Tiempo y Matemáticas, Bol. Soc. Esp. Mat. Apl. 22 (2002), 59-98.
[2] E. Lorenz, The Essence of Chaos, University of Washington Press, 1996.
Dejar una contestacion