
El 26 de abril de este año 2020 se cumplen 100 años del fallecimiento del genial matemático indio Srinivasa Ramanujan que, con una mínima educación académica, hizo contribuciones extraordinarias al análisis matemático, la teoría de números, las series y las fracciones continuas. Ramanujan había nacido el 22 de diciembre de 1887 y, tras años de trabajo autodidacta en la India, completamente aislado de la comunidad matemática, envió su famosa carta al matemático británico G. H. Hardy en enero de 1913, en la que le comunicaba unos cuantos de los resultados que había obtenido. Hardy reconoció el genio de Ramanujan y logró llevarlo a Cambridge, donde colaboraron durante casi cinco años. Enfermo —fue diagnosticado de tuberculosis, posiblemente de manera errónea—, volvió a la India en 1919, y murió poco después, a la edad de 32 años.
Además de las 37 publicaciones en revistas de investigación, 7 de ellas fruto de su colaboración con Hardy, nos dejó sus famosos «cuadernos», con una asombrosa colección de resultados poco convencionales, la mayor parte de ellos sin demostración alguna. Estudiar el contenido de estos cuadernos y proporcionar demostraciones rigurosas de las fórmulas allí recogidas ha sido objeto de estudio de numerosos matemáticos durante todo el siglo XX.
No es el objetivo de estas notas dar una visión de la vida y obra de Ramanujan sino, simplemente, mostrar el resultado más conocido que obtuvieron él y Hardy, y al que se alude repetidamente en la película biográfica «El hombre que conocía el infinito». Se trata del cálculo del número de particiones. Comenzaremos explicando el problema y analizando lo que se conocía antes de que Ramanujan entrara en escena, y en una próxima entrada finalizaremos con los avances de Hardy y Ramanujan, así como la mejora final de Rademacher.
Número de particiones
Dado \(n\) un número entero positivo, se llama partición de \(n\) a cualquier suma
\[ a_1 + a_2 + \cdots + a_r = n,\]
donde los \(a_j\) también son enteros positivos (no tienen por qué ser distintos unos de otros). Dos particiones que difieren solamente en el orden de los sumandos no se consideran distintas.
Si \(k_j\) es el número de veces que aparece \(a_j\) en la suma, también podemos poner
\[ k_1 a_1 + k_2 a_2 + \cdots + k_s a_s = n.\]
Aquí, los \(a_j\) ya son todos distintos, e incluso podemos pensar que en la suma participan todos los enteros \(a_j\), con todos los \(k_j = 0\) salvo un número finito.
Queremos conocer el número de particiones de \(n\), es decir, ¿de cuántas formas podemos escribir \(n\) como suma de enteros positivos? A ser número lo denotaremos mediante \(p(n)\).
Calcular el número de particiones es un problema de combinatoria nada sencillo. Su origen se remonta a Leibniz, que lo propuso en una carta fechada en 1696, y fue Euler el primero que hizo algunos progresos significativos en su estudio.
Para \(n\) pequeño, calcular \(p(n)\) a mano no tiene dificultad. Por ejemplo,
\[ 5 = 4 + 1 = 3 + 2 = 3+1+1 = 2+2+1 = 2+1+1+1 = 1+1+1+1+1,\]
así que \(p(5) = 7\).
Pero, como se ve en la siguiente tabla, el número de particiones crece bastante con \(n\), y no se observa ningún patrón:
\[
\begin{array}{rr@{\qquad\,}rr@{\qquad\,}rr@{\qquad\,}rr@{\qquad\,}rr}
\hline
n\; & p(n)\!\!\!\! & n\; & p(n)\! & n\; & p(n)\, & n\; & p(n)\,\, & n\; & p(n)\,\,\, \\
\hline
1 & 1 & 13 & 101 & 25 & 1958 & 37 & 21637 & 49 & 173525 \\
2 & 2 & 14 & 135 & 26 & 2436 & 38 & 26015 & 50 & 204226 \\
3 & 3 & 15 & 176 & 27 & 3010 & 39 & 31185 & 51 & 239943 \\
4 & 5 & 16 & 231 & 28 & 3718 & 40 & 37338 & 52 & 281589 \\
5 & 7 & 17 & 297 & 29 & 4565 & 41 & 44583 & 53 & 329931 \\
6 & 11 & 18 & 385 & 30 & 5604 & 42 & 53174 & 54 & 386155 \\
7 & 15 & 19 & 490 & 31 & 6842 & 43 & 63261 & 55 & 451276 \\
8 & 22 & 20 & 627 & 32 & 8349 & 44 & 75175 & 56 & 526823 \\
9 & 30 & 21 & 792 & 33 & 10143 & 45 & 89134 & 57 & 614154 \\
10 & 42 & 22 & 1002 & 34 & 12310 & 46 & 105558 & 58 & 715220 \\
11 & 56 & 23 & 1255 & 35 & 14883 & 47 & 124754 & 59 & 831820 \\
12 & 77 & 24 & 1575 & 36 & 17977 & 48 & 147273 & 60 & 966467 \\
\hline
\end{array}
\]
Dos son las preguntas clave que nos podemos hacer:
¿Existe alguna «fórmula cerrada» que proporcione \(p(n)\) para cualquier \(n\)?
¿Podemos estimar el tamaño de \(p(n)\) cuando \(n\) es grande?
El trabajo de Euler
La función generatriz de particiones
El primer avance importante en el estudio del número de particiones vino de la mano de Euler, pues consiguió escribir los \(p(n)\) por medio de una función generatriz.
Recordemos que, en general, se denomina función generatriz de una sucesión \(\{a(n)\}_{n=0}^{\infty}\) a una función \(G(x)\) cuyo desarrollo de Taylor es
\[ G(x) = \sum_{n=0}^{\infty} a(n) x^n.\]
Lo que Euler probó para el número de particiones \(p(n)\) es que, si además tomamos \(p(0) = 1\), se cumple
\[ \prod_{m=1}^{\infty} \frac{1}{1-x^{m}} = \sum_{n=0}^{\infty} p(n) x^n \]
para \(|x| < 1\).
En realidad, y si prescindimos de los detalles sobre convergencia, dicha fórmula no es difícil de probar. Si desarrollamos
\[ \prod_{m=1}^{\infty} \frac{1}{1-x^{m}} = (1+x+x^2+\cdots) (1+x^2+x^4+\cdots) (1+x^3+x^6+\cdots) \cdots \\ = 1 + \sum_{n=1}^{\infty} a(n) x^n, \]
queremos ver que \(a(n) = p(n)\).
Supongamos que hemos tomado el término \(x^{n_1}\) de la primera serie, \(x^{2n_2}\) de la segunda, \(x^{3n_3}\) de la tercera,… y el término \(x^{kn_k}\) de la \(k\)-ésima (con \(n_i\ge0\)). Su producto es \(x^{n_1} x^{2n_2} x^{3n_3} \cdots x^{kn_k} = x^n\), luego
\begin{align*}
n &= n_1 + 2n_2 + 3n_3 + \cdots + kn_k \\
&= (\underbrace{1+1+\cdots+1}_{n_1}) + (\underbrace{2+2+\cdots+2}_{n_2}) + \cdots
+ (\underbrace{k+k+\cdots+k}_{n_k}),
\end{align*}
y esto es una partición de \(n\) en sumandos positivos.
Cada partición de \(n\) producirá un término \(x^n\) y, recíprocamente, cada término \(x^n\) procede de una partición conveniente de \(n\). Por consiguiente, \(a(n)\) (el coeficiente de \(x^n\)) es igual a \(p(n)\) (el número de particiones de \(n\)), tal como buscábamos.
Relación con los números pentagonales
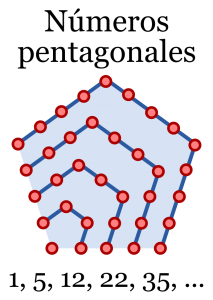
El siguiente paso para encontrar una fórmula para \(p(n)\) requiere, de manera sorprendente, hablar de los números pentagonales.
Por definición, el \(n\)-ésimo número pentagonal \(p_n\) es el número de puntos que hay en la superposición de \(n\) pentágonos regulares según el patrón que se muestra a la derecha.
Según se observa en el dibujo, cada nuevo pentágono añade \(4\) vértices y \(3\) aristas, así que
\[
p_n = p_{n-1} + 4 + 3(n-2).
\]
Por inducción (por ejemplo), obtenemos
\[
p_n = \frac{n(3n-1)}{2}, \quad n=1,2,3,\dots.
\]
Así, los primeros números pentagonales son
\[
1, 5, 12, 22, 35, 51, 70, 92,\dots
\]
Si en esa misma fórmula de los números pentagonales tomamos índices \(k \in \mathbb{Z}\) tenemos los denominados números pentagonales generalizados:
\[
g_k = \frac{k(3k-1)}{2}, \quad k = 0, 1, {-1}, 2, {-2}, 3, {-3},\dots
\]
Los primeros son
\[
0, 1, 2, 3, 5, 7, 12, 15, 22, 26, 35, 40, 51, 57, 70, 77, 92,\dots
\]
En 1750, Euler probó que, al multiplicar
\[
(1-x)(1-x^{2})(1-x^{3}) \cdots
= 1-x-x^{2}+x^{5}+x^{7}-x^{12}-x^{15}+x^{22}+\cdots
\]
muchos exponentes se cancelan, y los que quedan son precisamente los números pentagonales generalizados. En concreto, lo que se obtiene es el denominado teorema de los números pentagonales de Euler:
\[
\prod_{n=1}^{\infty} \left(1-x^{n}\right)
= \sum_{k=-\infty}^{\infty}(-1)^{k} x^{k(3 k-1)/2}.
\]
Este teorema tiene una gran importancia en el cálculo de \(p(n)\),
y son varias las formas de probarlo. Además de la demostración original de Euler (por inducción), existen demostraciones de Legendre (1830), Jacobi (1846) y Franklin (1881, con argumentos combinatorios).
Fórmula recursiva de Euler
Si utilizamos el teorema de los números pentagonales combinado con la función generatriz de las particiones, tenemos
\[
1 = \prod_{n=1}^{\infty} \left(1-x^{n}\right)
\prod_{m=1}^{\infty} \frac{1}{1-x^{m}}
= \Big(1 + \sum_{k=1}^{\infty}(-1)^{k} (x^{g_k} + x^{g_{-k}}) \Big)
\cdot \sum_{n=0}^{\infty} p(n) x^n.
\]
Multiplicar ambas expresiones nos lleva a que, si tomamos \(p(0) = 1\) y \(p(n) = 0\) si \(n<0\), para \(n \ge 1\) podemos escribir
\[
p(n) – p(n-1) – p(n-2) + p(n-5) + p(n-7) + \cdots = 0,
\]
o bien,
\[
p(n) = \sum_{k=1}^{\infty} (-1)^{k+1} \big(p(n-g_k)+p(n-g_{-k})\big)
\]
(a partir de un \(k\), los sumandos son todos nulos, luego esta serie es, realmente, una suma finita).
Esta fórmula recursiva, debida a Euler, permite calcular \(p(n)\) con relativa facilidad, y es lo mejor que había hasta que Ramanujan se interesó por el tema; lo que será considerado en una próxima entrada.
Muchos de los detalles del trabajo de Euler se pueden ver en [2]; en particular, en la magnífica edición facsímil (traducida y comentada) [3]. Si el lector está interesado en un tratamiento más actual, lo puede encontrar en [1].
Referencias
[1] T. M. Apostol, Introducción a la Teoría Analítica de Números, Reverté, Barcelona, 1980.
[2] L. Euler, Introductio in analysin infinitorum (1748), cap. 16, «De partitione numerorum», Opera omnia, ser.1, 8; «De partition enumerorum» (1753), Opera omnia, ser. 1, 2, p. 280.
[3] L. Euler, Introductio in analysin infinitorum, (Introducción al análisis de los infinitos), editado por A. J. Durán y F. J. Pérez, 2 vols. (facsímil y edición crítica), SAEM Thales y Real Sociedad Matemática Española, Sevilla, 2000.

Dejar una contestacion