Se trata de un problema simple, adictivo. El tipo de problemas que cualquiera puede entender. Con el último teorema de Fermat muchos se volvieron locos, espero no provocar este tipo de reacción. El problema es interesante y difícil y esto es casi lo único que sabemos…
Conjetura. Sea \(\mathcal F\) un conjunto finito de conjuntos finitos, cerrado para la unión, es decir, tal que si \(A, B\in\mathcal F\), entonces \(A\cup B\in \mathcal F\). Suponemos también que \(\mathcal F\) contiene algún conjunto no vacío. Entonces existe un elemento \(x\) tal que pertenece al menos a la mitad de los conjuntos de \(\mathcal F\). Esto es, $$\mathop{\rm card}(\{A\in\mathcal F\colon x\in A\})\ge \frac12\mathop{\rm card}(\mathcal F).$$
La primera reacción puede ser de incredulidad o bien pensar que tiene que ser fácil de probar si es que es cierto. Ya lo dije antes, por los ejemplos parece cierto, pero podemos estar seguros de que no es fácil… Pero seguro que ya alguno está tratando de encontrar una estrategia para probarlo.
Antes de explicar lo poco que sabemos sobre este problema, voy a hablar del matemático que formuló la pregunta, un matemático poco típico.
Peter Frankl
Sus padres estuvieron en campos de concentración nazi, perdieron todas sus pertenencias y, sobre todo, a muchos familiares, pero ellos pudieron escapar. Cuánto les afectó se muestra hasta en la elección del nombre de su hijo. Su padre quiso que se llamara Aaron, pero su madre se opuso fuertemente prefiriendo un nombre, Peter, que no delatara sus raíces. Su padre le decía «Peter, tan solo los conocimientos en tu mente y los sentimientos de tu corazón te pertenecen realmente».
Nació en 1953 en un pueblecito de Hungría. Destacó desde muy niño, por ejemplo, con cuatro años multiplicaba mentalmente números de 2 cifras. En otra entrada, The happy end problem, hablé de la matemática húngara y de cómo la sociedad húngara valora el talento. Peter es un ejemplo de cómo esta política potencia a las personas, obtuvo una medalla de oro en la Olimpiada Matemática Internacional en 1971. A esa edad de 18 años se decidió por estudiar matemáticas en la Universidad Eötvös Loránd en Budapest presentando su tesis doctoral antes de obtener el título.

Fue a Francia a estudiar en París en 1975, le impresionó mucho la libertad de los países occidentales, sobre todo la libertad de viajar. Se nacionalizó francés y desde entonces no ha dejado de viajar Reino Unido, India, Estados Unidos, y un largo etcétera. Trabajó con Paul Erdös y Ronald Graham. De Ronald Graham además de matemáticas tomó la afición por los juegos malabares, que también le han acompañado toda su vida. Es frecuente que en sus charlas mezcle las matemáticas con los malabares. Sus trabajos matemáticos en el campo de la combinatoria son muchos e importantes, por ejemplo resolvió una conjetura que Erdös valoraba en 1000 $. Formuló la conjetura que hoy comentamos en 1979 en un viaje de París a Toronto.
En uno de sus viajes a Japón quedó impresionado, tanto que en pocos años se mudó allí, y desde 1988 vive en Japón, donde ha llegado a ser un personaje muy conocido. Dirige el equipo japonés de las Olimpiadas Matemáticas y es frecuente verlo en la televisión. Al comienzo fue a Japón con una beca, pero cuando esta acabó y decidió afincarse en Japón también decidió vivir libre de un trabajo, subsistiendo al principio con actuaciones con juegos malabares y más adelante con la publicación de libros y conferencias, no dejando en ningún momento la investigación matemática.
Su página web está toda ella en Japonés. Para Peter los idiomas son como camisas. Habla 12 idiomas: húngaro, inglés, ruso, sueco, francés, español, polaco, alemán, japonés, chino, thai y coreano. Ha viajado a mas de 100 países y dado conferencias en esos idiomas.
¿Qué sabemos de la conjetura?
La conjetura es cierta si en la familia \(\mathcal F\) hay un conjunto unitario \(\{a\}\). La prueba es muy simple, por cada conjunto \(A\in\mathcal F\) que no contenga a \(a\), tenemos el conjunto \(\{a\}\cup A\in\mathcal F\) que sí lo contiene. Luego son más de la mitad los que contienen a \(a\).
La conjetura es cierta si en la familia \(\mathcal F\) hay un conjunto \(\{a,b\}\) con dos elementos. En efecto, podemos dividir la familia \(\mathcal F\) en cuatro partes disjuntas \(\mathcal F_{a,b}\cup\mathcal F_a \cup \mathcal F_b\cup \mathcal F_0\) según si contienen a los dos elementos \(a\) y \(b\), solo a \(a\), solo a \(b\) o a ninguno. \(\mathcal F_{a,b}\) contiene más elementos que \(\mathcal F_0\), pues por cada \(A\in \mathcal F_0\) tenemos \(A\cup\{a,b\}\in \mathcal F_{a,b}\). Ahora, uno de \(\mathcal F_a\) o \(\mathcal F_b\) contiene igual o más elementos que el otro. Por ejemplo, si es \(\mathcal F_a\), tendremos que \(a\) está en cada conjunto de \(\mathcal F_{a,b}\cup\mathcal F_a\) y esos son más de la mitad del total.
Este tipo de razonamiento se acaba aquí. Hay ejemplos en que \(\{a,b,c\}\in \mathcal F\) pero ni \(a\), ni \(b\), ni \(c\) está en más de la mitad de los conjuntos de \(\mathcal F\). Pero los matemáticos son tan perseverantes… Sabiendo de este ejemplo, Bjorn Poonen, cuando todavía era un estudiante, prueba el siguiente resultado:
Proposición. Si hay cuatro elementos tales que \(\{a,b,c\}\), \(\{a,b,d\}\) y \(\{a,c,d\}\) están en \(\mathcal F\), entonces uno de los cuatro elementos \(a\), \(b\), \(c\) o \(d\) está en más de la mitad de los elementos de \(\mathcal F\).
Algo de notación. Para hablar del siguiente resultado debemos introducir dos números asociados al problema. Sea \(\mathcal F\) una familia finita de conjuntos finitos cerrados para la unión. La unión de todos los conjuntos de la familia, \(X\), está en la familia, y todos los conjuntos de \(\mathcal F\) son subconjuntos de \(X\). Designaremos por \(M\) el cardinal de \(X\) y por \(N\) el número de conjuntos de la familia. También designaremos por \(N_j\) el número de elementos de \(\mathcal F\) con justamente \(j\) elementos. Finalmente, si \(a\in X\) designaremos por \(\mathcal F_a\) la familia de conjuntos de \(\mathcal F\) que contienen a \(a\).
La conjetura dice entonces que si \(\mathcal F\) es una familia finita de conjuntos finitos cerrada para la unión y conteniendo algún conjunto no vacío, entonces existe \(a\in X\) tal que el cardinal de \(\mathcal F_a\) es \(\ge N/2\).
Bjorn Poonen prueba entonces
Lema. Si una familia \(\mathcal F\) satisface \(\sum_{j=1}^{M-1}(j-M/2)N_j\ge0\), entonces la conjetura es cierta para esta familia.
Basta ver que la desigualdad anterior expresa que la media de los cardinales de \(\mathcal F_a\) es mayor que \(N/2\). Con esto demuestra las siguientes proposiciones:
Proposición. La conjetura es válida para \(\mathcal F\) si \(M\le 7\), es decir, si solo intervienen 7 elementos o menos en los conjuntos de \(\mathcal F\).
Proposición. La conjetura es válida si \(N\le 28\). Esto es, si \(\mathcal F\) contiene a lo sumo 28 conjuntos.
Estos resultados de Poonen se han mejorado, actualmente sabemos que la conjetura es válida si \(M\le 12\) o \(N\le 50\), o cuando hay muchos conjuntos; \(N\ge \frac232^M\).
El resultado positivo mas general sobre la conjetura es que siempre existe un \(x\in X\) tal que está en \(\ge \frac{N-1}{\log_2N}\) conjuntos de la familia.
La Conjetura en Retículos
Podemos formar un grafo a partir de la familia \(\mathcal F\) cerrada por uniones. Los vértices son los conjuntos en \(\mathcal F\) y dos vértices \(A\ne B\) están conectados si \(A\subset B\) y cualquier conjunto \(C\) de la familia tal que \(A\subset C\subset B\) coincide con \(A\) o con \(B\). Podemos formular la conjetura en función de este grafo o del retículo definido por \(A\le B\) si y solo si \(A\subset B\). Poonen estudia estas equivalencias y prueba la conjetura para retículos con ciertas propiedades.
Por ejemplo, con \(X=\{1,2,3,4,5,6,7,8,9\}\) tenemos una familia que tiene el grafo:
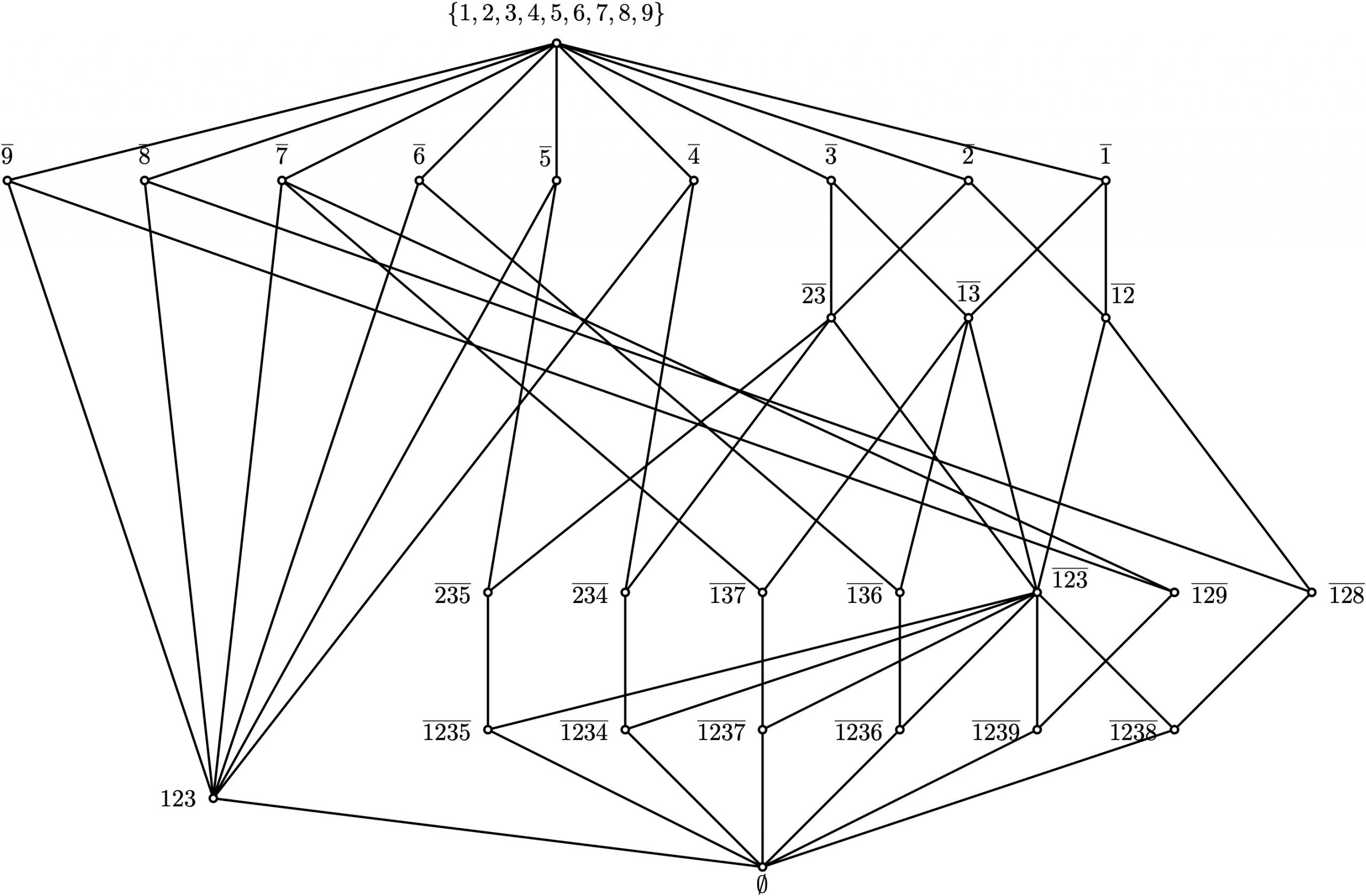
En la figura, \(123\) denota el conjunto con esos tres elementos y \(\overline{1235}\) denota el complemento en $X$ del conjunto \(\{1,2,3,5\}\), es decir, el conjunto \(\{4,6,7,8,9\}\). En este ejemplo, el cardinal de \(X\) es \(N=9\) y la familia está formada por \(M=28\) conjuntos.
El menor conjunto en este ejemplo es \(\{1,2,3\}\) pero ni \(1\) ni \(2\) ni \(3\) sirven en la conjetura, pues cada uno de ellos esta en solo 13 conjuntos. Pero, por ejemplo, \(5\) está en 24 conjuntos.
Polymath, una medida de la dificultad del problema
Una medida de lo complicado del problema la puede dar el proyecto de Gowers. Timothy Gowers fue medalla Fields en 1998 por sus trabajos en combinatoria y análisis funcional. Gowers ha generado unos proyectos (Polymath) en la red, en la que matemáticos de todo el mundo colaboran y ponen en común sus ideas para la solución de problemas matemáticos, en algunos casos con gran éxito. Una de estos proyectos se dedicó a la conjetura de Frankl. Plantearon diversas estrategias y metas parciales. Por ejemplo, trataron de probar que al menos hay un elemento \(x\) que esté en una proporción fija del número de conjuntos, digamos que \(\ge N/1000\) conjuntos de la familia. Al final del proyecto solo quedó un conjunto de ideas, que nadie consiguió convertir en una prueba, pero que sin duda son interesantes para cualquiera interesado en resolver el problema. (Quizás para evitar caminos infructuosos, pero posiblemente para tomar ideas que potencialmente son interesantes.)
Gil Kalai comentó en el blog de Gowers:
Hace años Jeff Kahn me propuso una apuesta de que encontraría contraejemplos a cada reforzamiento de la conjetura de Frankl que tuviera sentido. Y, en efecto, pulverizó muchas de las que propuse, incluyendo algunas con pesos. […] Parece que encontrar una conjetura que implique la de Frankl y no sea obviamente falsa (al menos para Jeff Kahn) sería un logro.
En el blog de Gowers habían conseguido un logro de este tipo, en el sentido de que habían dado con un enunciado que implica la conjetura de Frankl y sobre la que Jeff Kahn pensaba que era falsa, pero no podía dar un contraejemplo.
Yo propongo aquí una conjetura, más fuerte que la de Frankl y que no he pensado lo suficiente, de manera que un lector podría sin mucha dificultad encontrar un contraejemplo.
Conjetura poco pensada. Si tengo un conjunto de funciones positivas y medibles, \(f_1,\ldots,f_N\colon[0,1]\to [0,+\infty)\), cerradas para el supremo, es decir, que \(\sup(f_i,f_j)\) es siempre igual a alguna \(f_k\), entonces $$\Bigl\Vert\sum_{j=1}^N f_j\Bigr\Vert_\infty\ge\frac12\sum_{j=1}^N \Vert f_j\Vert_\infty.$$
La conjetura de Frankl resulta un caso particular cuando tomamos funciones escalonadas características de conjuntos.
Para saber más
La conjetura ha tenido mucha publicidad. Un buen estudio se encuentra en arXiv, cita 72 trabajos, lo que puede dar una medida de la atención que ha recibido la conjetura:
H. Bruhn y O. Schaudt, The journey of the union-closed sets conjecture, arXiv: 1309.3297.
Gowers propone su proyecto sobre la conjetura en Frankl’s union-closed conjecture—a possible Polymath project?, sus primeras conclusiones se pueden ver en la entrada de su blog FUNC1—strengthenings, variants, potential counterexamples y sobre todo en la página wiki del proyecto.
La página web de Peter tiene poca información aparte de una lista de trabajos. Mucho más interesante es la que tiene en japonés. Podemos ver a Peter hablando de combinatoria y su conjetura, así como realizando juegos malabares en inglés, en ruso, en chino o simplemente actuando en youtube.
Bjorn Poonen obtuvo una medalla de plata en la Olimpiada Matemática Internacional de 1985 y su trabajo sobre la conjetura de Frankl los realizó antes de doctorarse. Su artículo puede descargarse libremente en la red:
B. Poonen, Union closed families, J. Combin. Theory A, 59 (1992) 253–268.
Hay muchos trabajos y documentos accesibles en la red sobre esta conjetura.
El título «Conjetura diabólica» lo he tomado del gran libro Enumerative Combinatorics de Richard Peter Stanley.
Uno de los motivos de Peter Frankl para quedarse en Japón son sus jardines. Hemos tomado la figura destacada de uno de ellos: Koishikawa Korakuen.

Dejar una contestacion