La conjetura de Sendov

Entre los objetos más sencillos de las matemáticas se encuentran los polinomios en una variable. Los chavales los estudian en los colegios e institutos y, al menos muchos, aprenden a operar con ellos y comprenden bastantes de sus propiedades. Con respecto a los puntos en los que se anulan los polinomios (denominados ceros o raíces), saben cómo calcularlos para polinomios de grados 1 y 2, y para polinomios de grados más altos en algunos casos. También estudian el teorema de Bolzano.

Si nos colocamos en un nivel académico más elevado, hay multitud de propiedades conocidas de los ceros de los polinomios. La más importante es que un polinomio de grado \(n\) tiene siempre exactamente \(n\) raíces complejas (contando su multiplicidad). Otros resultados bien conocidos son, por citar unos pocos, las fórmulas de Vieta-Cardano, la regla de los signos de Descartes y los teoremas de Sturm, Lagrange y Cauchy para localizar las raíces, el teorema de Gauss-Lucas sobre los ceros de la derivada, etcétera.

Pero lo que aquí nos interesa es que también existen propiedades que no se sabe si son ciertas o no. En matemáticas, normalmente no es fácil enunciar preguntas comprensibles por no especialistas cuya respuesta sea incierta. En esto, la teoría de números es una clara excepción, donde son numerosas las preguntas relativamente sencillas cuya respuesta no se conoce. Lo que ahora vamos a ver es un problema abierto relacionado con las raíces de polinomios y que, para comprender su enunciado, basta con conocer lo que es el plano complejo.

El problema se le ocurrió al búlgaro Blagovest Sendov en 1959. En esa época, Sendov era un joven profesor de matemáticas en la Universidad de Sofía; en concreto, se había especializado en métodos numéricos y matemática computacional. Años más tarde fue rector de su universidad y miembro de la Academia Búlgara de Ciencias; también se interesó por la política (llegó a ser presidente del parlamento búlgaro), y fue embajador de Bulgaria en Japón. Falleció en enero de 2020 (véase [2]), así que no tuvo ocasión de disfrutar de la pandemia que nos tiene ahora a todos entretenidos. Lo que Sendov conjeturó fue lo siguiente:

Conjetura de Sendov (1959): Sea \(f: \mathbb{C} \to \mathbb{C}\) un polinomio de grado \(n \ge 2\) cuyos ceros están todos en el círculo unidad (cerrado); entonces, para cualquier cero \(z_0\) de \(f(z)\), el círculo (cerrado) de centro \(z_0\) y radio \(1\) contiene, al menos, un cero de la derivada \(f'(z)\).

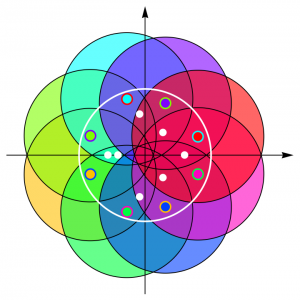
En la figura adjunta se puede ver un ejemplo de la situación con el polinomio \(f(z) = z^8 – 17 z^4/72 + z^3/16 – z/12 + 81/256\), cuyos ocho ceros, de colores, están todos dentro de la circunferencia unidad (señalada en blanco). Alrededor de cada cero se muestra, del mismo color que el cero, el círculo de radio \(1\) centrado en él. Como se puede apreciar, todos esos círculos contienen, al menos, uno de los siete ceros de \(f'(z)\), que están representados en blanco.

A quien primero transmitió Sendov su conjetura fue a su colega Nikola Obreshkov. También llegó a oídos de Ljubomir Iliev, quien, bien relacionado con la comunidad matemática, la comentó con bastantes más matemáticos. En particular, lo hizo en una conferencia en Erevan en 1965, citando a su autor. Nos podemos imaginar a Iliev por la tarde, de tapas en un bar después de asistir a las charlas del congreso, explicándole a un amigo la conjetura a ver si sabían dar con un contraejemplo o una demostración. Así la conjetura llegó a Walter Hayman, quien la incluyó en su libro [1, Problem 4.5] (publicado en 1967); pero Hayman había olvidado que el problema lo había propuesto Sendov y se lo atribuyó a Iliev. Esa fue la primera vez que la conjetura se plasmaba por escrito, aunque con el nombre de conjetura de Iliev, con el que fue conocida durante varios años (a veces también se la denomina conjetura de Iliev-Sendov). Se pueden ver más detalles de esta historia en [3] y [2].

La conjetura de Sendov continúa siendo un problema abierto, pero desde que se propuso se han producido avances significativos en pos de su solución. Merece la pena mencionar algunos de estos progresos:

• 1969: Amram Meir y Ambikeshwar Sharmaand prueban la conjetura para polinomios de grado \(n \le 5\).
• 1991: Johnny E. Brown extiende la demostración al caso \(n \le 6\).
• 1996: Iulius Borcea da otra demostración del caso \(n \le 6\), y también consigue probar el caso \(n \le 7\).
• 1997: Brown da una demostración independiente del caso \(n \le 7\).
• 1999: Brown y su estudiante Guangping Xiang alcanzan el caso \(n \le 8\).
• 2014: Jérôme Dégot prueba que la conjetura es cierta para \(n\) suficientemente grande, pero dependiente del cero \(z_0\).

Aclaremos un poco más lo que quiere decir el último punto. Al estudiar la conjetura, se puede considerar que el polinomio es mónico y rotar el cero \(z_0\) de manera que esté situado en el intervalo \([0,1]\). De esta forma, al cero lo denominamos \(a\), y se puede analizar la conjetura haciéndola depender de \(a\) (por supuesto, el objetivo sería demostrarla para todo \(a\) y todo \(n\)).

Con esta interpretación, la conjetura para \(a=0\) resulta ser el teorema de Gauss-Lucas (los ceros de la derivada están en la envoltura convexa de los ceros del polinomio). Asimismo, Borislav Bojanov había demostrado en 2011 que la conjetura era cierta para \(a \le 1/(n-1)\); y Tomohiro Chijiwa que lo era para \(a \ge 1 – 1/(2^{2n+1}n^9)\) (Indraneel Kasmalkar extendió esto hasta \(a \ge 1 – 90/(n^{12}\log n)\) en 2014).

Lo que Dégot probó en 2014 es que, para cada \(c \in (0,1/2]\), y si el cero \(a\) cumple \(c \le a \le 1-c\), la conjetura se cumple para \(n\) suficientemente grande (dependiente de \(c\)). En 2020, T. P. Chalebgwa extendió la demostración al caso \(C n^{-1/7} \le a \le 1 – Cn^{-1/4}\), para \(C\) una constante absoluta suficientemente grande.

En los resultados anteriores la demostración de la conjetura de Sendov para \(n\) suficientemente grande no era muy satisfactoria, pues dependía de la posición del cero. Para \(a\) muy cercano a \(0\) o a \(1\), la conjetura para \(n\) suficientemente grande permanecía en duda. Fue a final de 2020 cuando entra en escena Terence Tao. En su artículo [4] que, de momento, solo está publicado en arXiv, Tao de nuevo sorprende a la comunidad matemática con un avance sustancial, pues logra probar que existe una constante absoluta \(n_0\) (es decir, sin hipótesis adicionales sobre la posición del cero) tal que la conjetura de Sendov es cierta para polinomios de grado \(n \ge n_0\). Además de en [4], se pueden ver más detalles de la demostración de Tao en su blog [5].

Por supuesto, todavía queda un gran trecho hasta la demostración completa. En particular, aunque Tao prueba la existencia de la constante \(n_0\), no da un valor explícito para dicha constante. Incluso así, aún permanecería abierto el caso \(9 \le n < n_0\). ¿Por cuánto tiempo?

Referencias

[1] K. Hayman, Research Problems in Function Theory, Althlone Press, Londres, 1967.

[2] Ivanov y P. Petrushev, In Memoriam: Blagovest Sendov February 8, 1932-January 19, 2020, J. Approx. Theory 254 (2020), 105406, 27 pp.

[3] Bl. Sendov, Generalization of a conjecture in the geometry of polynomials, Serdica Math. J. 28 (2002), 283-304.

[4] T. Tao, Sendov’s conjecture for sufficiently high degree polynomials, arXiv:2012.04125, 2020, 36 pp.

[5] T. Tao, Sendov’s conjecture for sufficiently high degree polynomials, 8 de diciembre de 2020.