Un \(83.3\%\) de los lectores de la sección «Terra incognita» de este blog se podían haber saltado este párrafo introductorio, pues saben perfectamente la historia de que, en el Congreso Mundial de Matemáticos que se celebró en París en 1900, el eminente matemático alemán David Hilbert expuso una lista de 23 problemas matemáticos cuya solución no era conocida, y que esta recopilación de problemas ha resultado muy influyente en la investigación matemática del siglo XX. Pese a los esfuerzos invertidos por numerosas mentes brillantes, varios de esos problemas permanecen aún sin resolver.
Por supuesto, la estadística anterior es inventada, pero no tiene menos fiabilidad que la de muchas de las encuestas electorales que se publican. Y, si la estadística no hubiera sido inventada, no cuesta nada darse cuenta de que el dato \(83.3\%\) proviene de la fracción \(5/6 = 0.83333\dots\), así que habría sido una encuesta hecha a \(6\) personas, \(5\) de las cuales conocían la historia. De hecho, es lo que pasa con las encuestas a nivel español cuando se desglosan por comunidades autónomas y aparecen los datos de la del autor de este escrito (La Rioja).
Uno de los 23 problemas que permanece sin resolver es el 16, titulado «Problema de la topología de las curvas y superficies algebraicas». El enunciado preciso de ese problema, tal como lo propuso Hilbert, se puede encontrar en [13]. De hecho, ese artículo contiene mucha más información que la que aquí vamos a exponer; también [6, 7, 8] y sus referencias son útiles para profundizar en el tema y para conocer variantes que han atraído la atención de los investigadores.
Hay que aclarar que el problema tiene dos partes que, aunque tienen conexión, están bien diferenciadas. Incluso pertenecen a ramas distintas de las matemáticas (geometría algebraica real la primera, y sistemas dinámicos o ecuaciones diferenciales la segunda):
- Una investigación de las posiciones relativas de las ramas de las curvas algebraicas reales de grado \(n\) (y, de manera similar, para las superficies algebraicas).
- La determinación del límite superior para el número de ciclos límite en campos vectoriales bidimensionales polinómicos de grado \(d\), y una investigación de sus posiciones relativas.
Aquí sólo nos vamos a preocupar de la segunda parte.
Cíclos límite
Por comodidad, de aquí en adelante usaremos simplemente \(x=x(t)\) e \(y=y(t)\) para denotar funciones de variable real, y \(x’ = x'(t) = \frac{dx}{dt}\) e \(y’ = y'(t) = \frac{dy}{dt}\) serán sus derivadas. Así, consideraremos sistemas de ecuaciones diferenciales de la forma
$$
\tag{1}
x’ = P(x,y), \quad y’ = Q(x,y),
$$
donde \(P\) y \(Q\) son polinomios de grado menor o igual que \(d\). Cuando \(d=1\), el estudio de lo que sucede es sencillo y bien conocido, y se puede encontrar en muchos textos (véase, por ejemplo, [18, §42]); las dificultades surgen cuando \(d \ge 2\). Antes de proseguir, y para quien no esté familiarizado con la teoría cualitativa de las ecuaciones diferenciales, conviene explicar qué son los ciclos límite a los que alude el problema.
En la ecuación (1), si tomamos \(t_0 \in \mathbb{R}\) y \((x_0,y_0) \in \mathbb{R}^2\), podemos pensar en el problema de valores iniciales
$$
\begin{aligned}
\begin{cases}
x’ = P(x,y), \quad y’ = Q(x,y) \\
x(t_0) = x_0, \quad y(t_0) = y_0,
\end{cases}
\end{aligned}
$$
cuya solución \((x(t),y(t))\) será una curva (paramétrica) en el plano \(\mathbb{R}^2\); como la ecuación diferencial es autónoma (esto es, \(P\) y \(Q\) no dependen de \(t\)), el valor inicial \(t_0\) no tiene importancia, y el dibujo de la solución \((x(t),y(t))\), \(t \in \mathbb{R}\), será el mismo independientemente de cuál sea \(t_0\) (con lo cual se puede tomar \(t_0=0\)). Esas curvas se denominan órbitas o trayectorias.
Un ejemplo muy sencillo es la ecuación
$$
\tag{2}
x’ = x,\quad y’ = x+y,
$$
que tiene como soluciones, además de la solución constante \((x(t),y(t)) = (0,0)\) (que se denomina punto crítico, punto de equilibrio o punto fijo, y que surge cuando se toma el valor inicial \((x_0,y_0)=(0,0)\)), las funciones
$$
x(t) = c_1e^t,
\quad
y(t) = (c_1t+c_2)e^t
$$
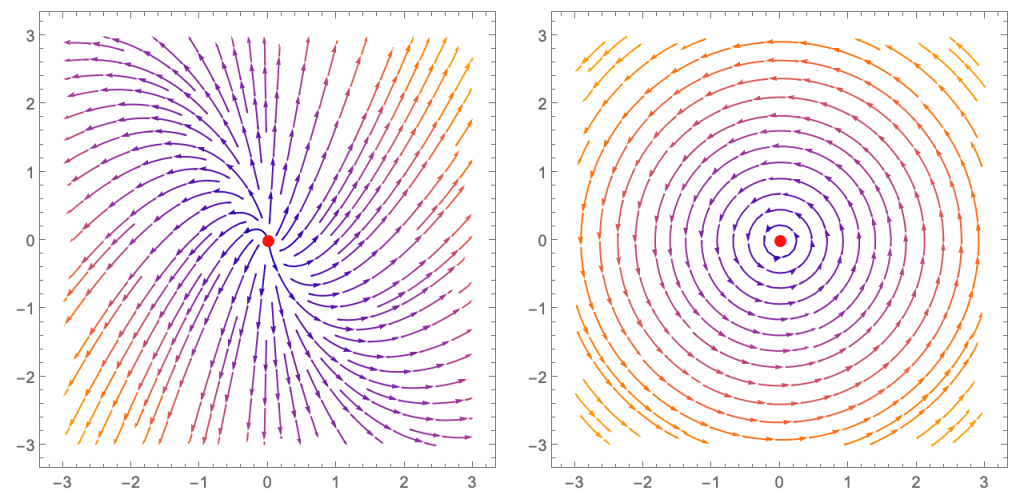
(donde \(c_1\) y \(c_2\) son constantes que dependen de \(t_0,x_0,y_0\)). Son las curvas que se pueden observar en la figura 1 (las fechas indican el avance de las trayectorias cuando crece la variable \(t\)); el punto crítico está representado en rojo.
Una solución, en ocasiones, puede ser periódica y, en ese caso, la trayectoria se denomina órbita periódica o ciclo. Por ejemplo, en la ecuación
$$
\tag{3}
x’ = -2y,\quad y’ = 2x,
$$
una solución es la constante \((x(t),y(t))=(0,0)\) (punto crítico), y las soluciones se pueden expresar en la forma
$$
x(t) = c \cos(2t+b),
\quad
y(t) = c \operatorname{sen}(2t+b)
$$
(las constantes \(b\) y \(c\) dependen de \(t_0,x_0,y_0\)), y son circunferencias centradas en el origen y radio \(|c|\); véase la figura 2. En este caso, todas las soluciones son periódicas (para cualquier valor inicial \((x_0,y_0)\) que tomemos, la solución es la circunferencia que pasa por el punto \((x_0,y_0)\), que da infinitas vueltas sobre sí misma cuando \(t\) varía en \(\mathbb{R}\)).
La ecuación
$$
\tag{4}
x’ = -y + x(1-x^2-y^2), \quad y’ = x + y(1-x^2-y^2)
$$
representa mejor lo que queremos estudiar. Además del consabido punto crítico en el que ya no insistiremos, sus soluciones son curvas paramétricas
$$
x(t) = \frac{\cos(t+b)}{\sqrt{1+ce^{-2t}}},
\quad
y(t) = \frac{\operatorname{sen}(t+b)}{\sqrt{1+ce^{-2t}}}
$$
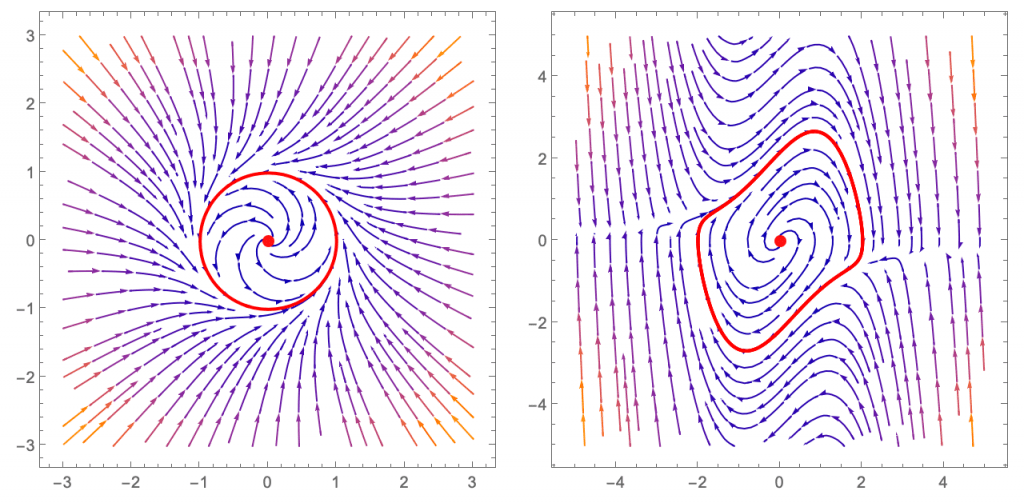
con \(c\) un número real (que depende del valor inicial \((x_0,y_0)\)). Si \(c=0\), esa trayectoria es la circunferencia \(x^2+y^2=1\). Si \(c < 0\), la trayectoria es una curva que está en el exterior de la circunferencia y que se acerca a ella (dando vueltas alrededor) cuando \(t\to\infty\). Finalmente, si \(c > 0\), es una curva interior a la circunferencia y que se acerca a ella (dando vueltas por el interior) cuando \(t \to \infty\). Esta vez, sólo hay una trayectoria periódica, la que se corresponde con \(c=0\). Puede verse, en rojo, en la figura 3 (también está en rojo el punto crítico).
En ocasiones (de hecho, es lo más habitual), ni siquiera podemos dar una expresión explícita para las soluciones de la ecuación diferencial. Éste es el caso de la ecuación
$$
\tag{5}
x’ = y,\quad y’ = -x + \mu(1-x^2)y,
$$
donde \(\mu\) es un parámetro real positivo, que se denomina ecuación de Van der Pol. Como se ve en la figura 4 (en la que hemos tomado \(\mu=1\)), hay una trayectoria periódica, y las demás trayectorias se aproximan a ella, unas por fuera y otras por dentro.
La noción de ciclo límite apareció entre los años 1891 y 1897 en los trabajos de Poincaré sobre la dinámica de las ecuaciones diferenciales. En concreto, se denomina ciclo límite a una órbita periódica de la ecuación (1) que esté aislada en el conjunto de todas las órbitas periódicas de la ecuación. En el caso (3) no hay ciclos límite (los ciclos no están aislados unos de otros); pero sí los hay en los casos (4) y (5).
Un ejemplo con más de un ciclo límite es la ecuación
$$
\tag{6}
\begin{aligned}
x’ &= -y + x\big((x^2+y^2)^2-5(x^2+y^2)+4\big),\\
y’ &= x + y\big((x^2+y^2)^2-5(x^2+y^2)+4\big).
\end{aligned}
$$
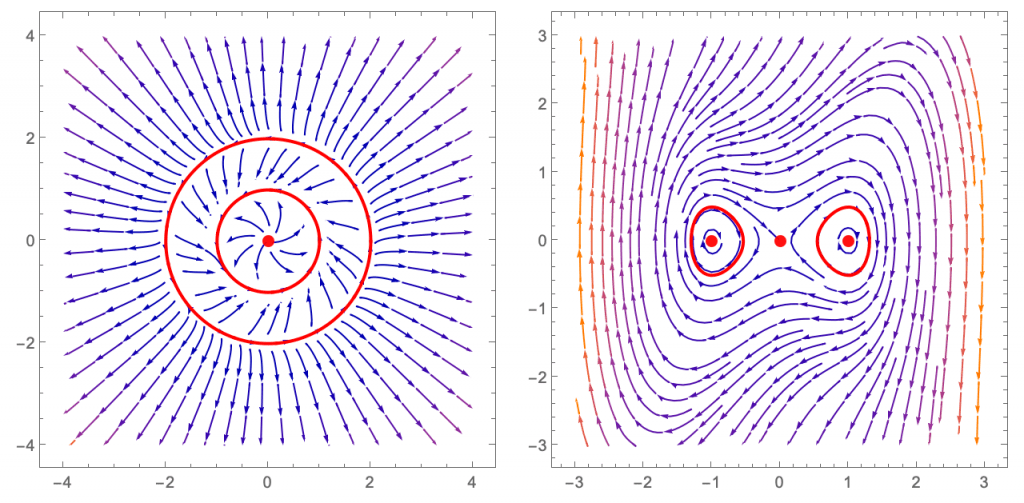
Tiene dos ciclos límite que son las circunferencias \(x^2+y^2 = 1\) y \(x^2+y^2 = 4\) de \(\mathbb{R}^2\). Se puede ver en la figura 5.
Otro ejemplo con dos ciclos límite es la ecuación
$$
\tag{7}
x’ = 2y(10+xy),\quad y’ = 20x + y – 20x^3 – 2x^2y + 4y^3,
$$
cuyos ciclos límite son las dos componentes de la curva algebraica de ecuación \(2x^4 – 4x^2 + 4y^2 + 1 = 0\) en \(\mathbb{R}^2\). Como se puede ver en la figura 6, esta vez los dos ciclos no están uno dentro del otro (además, aparte del punto crítico \((0,0)\), cada ciclo tiene otro punto crítico en su interior). Al contrario de lo que ocurre en los anteriores ejemplos (4) y (6) o en éste (que proviene de [15, proposición 19]), es muy excepcional que los ciclos límite tengan una expresión algebraica; en ocasiones, como se muestra en [9], incluso se puede probar explícitamente que el ciclo límite no es una curva algebraica (que el ciclo límite de la ecuación de Van der Pol (5) no es algebraico lo demostró Odani en 1985, [16]).
Es relevante mencionar que, en sus orígenes, el estudio de los ciclos límite tenía un interés puramente matemático, y proveniente, sobre todo, de su relación con el teorema de Poincaré-Bendixson. Pero Van der Pol en 1927 con su ecuación (5), y algunos otros investigadores un poco después, encontraron que, en ciertos circuitos eléctricos con válvulas de vacío, aparecía una oscilación estable (solución periódica) que era un ciclo límite en el sentido definido por Poincaré. Tras la comprobación de la existencia de ciclos límite en la naturaleza, la existencia, no existencia, estabilidad, unicidad y otras propiedades de los ciclos límite comenzaron a ser de interés no sólo para matemáticos —que ya estaban motivados gracias a los trabajos de Poincaré y Hilbert—, sino para físicos e ingenieros y, más tarde, para los estudiosos de otras ciencias, como biología, economía, epidemiología, química y sismología, entre otras.
La principal dificultad del problema es que, dada una ecuación diferencial concreta en el plano (polinomial o no, sin ningún parámetro), no hay ninguna técnica universal que sirva para acotar el número de ciclos límite que tiene (y mucho menos dar el número exacto). Hay varios criterios de no existencia de ciclos límite, o de unicidad de ciclos límite, y eso permite determinar el número de ciclos (uno o ninguno) en muchas ecuaciones. Pero, por ejemplo, son muy pocos los casos en los que se ha podido demostrar la existencia de exactamente dos ciclos límite.
Si no exigimos que \(P\) y \(Q\) en (1) sean polinomios, sino funciones analíticas, existen ejemplos sencillos de ecuaciones con infinitos ciclos límite. Por ejemplo, la ecuación diferencial
$$
x’ = -y + x\operatorname{sen}(x^2+y^2), \quad y’ = x + y\operatorname{sen}(x^2+y^2)
$$
tiene como ciclos límite las circunferencias \(x^2+y^2=k\pi\) con \(k\) entero positivo. Ésta es la razón por la que en el problema de determinar el número de ciclos se exige que \(P\) y \(Q\) sean polinomios.
En 1923, Dulac [4] afirmó haber probado que una ecuación diferencial polinomial (1) sólo puede tener un número finito de ciclos límite (quizás ninguno, claro). Pero, en 1985, Ilyashenko [11] encontró un error en el trabajo de Dulac (previamente también se habían encontrado fallos, e incluso contraejemplos, en otros intentos de demostración de otros autores que, durante algunos años, se habían considerado correctos). No mucho después se publicaron dos largos trabajos que probaban la afirmación de Dulac: uno se debe al propio Ilyashenko [12] (en 1991) y el otro a Écalle [5] (en 1992). En palabras de Smale en 1998 [19, 20], «la comunidad matemática aún tiene que digerir a fondo estos dos artículos», lo cual apuntaba a que a nadie le extrañaría sobremanera que aparecieran nuevos errores; de hecho, recientemente se ha descubierto un fallo en la demostración de [12], que Ilyashenko ha reconocido y está intentando corregir (para más detalles, véase [8]).
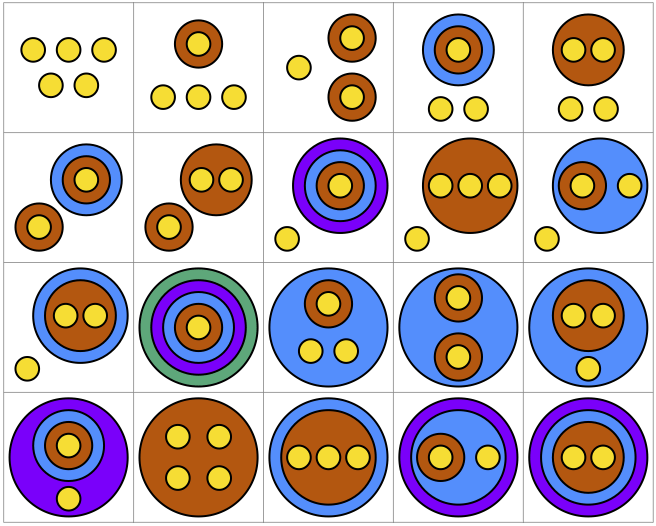
En cuanto a la posición relativa de los distintos ciclos límite, nos podemos preguntar, por ejemplo, si hay ciclos límite unos dentro de otros (nidos de ciclos límite), y cuántos puede haber. En general, cuáles son las posibles distribuciones o configuraciones topológicas de los ciclos límite (tanto en (6) como en (7) hay dos ciclos pero, a la vista de las figuras 5 y 6, su configuración topológica es claramente distinta). A este respecto, se puede consultar [3, 14, 10]. No proseguiremos más por este camino, pero sí comentaremos que, cuantos más ciclos límite hay, mayor es el número de configuraciones topológicamente distintas que pueden adoptar. Por ejemplo, con 2 ciclos hay 2 configuraciones; con 3 ciclos, 4 configuraciones; con 4 ciclos, 9 configuraciones; con 5 ciclos, 20 configuraciones; y con 6 ciclos, 48 configuraciones. La figura 7 (que está extraída de [10]) muestra, de manera esquemática, las 20 configuraciones que pueden adoptar 5 ciclos límite (los colores son puramente ilustrativos, no tienen ningún significado en la dinámica del problema); todas ellas se pueden obtener mediante sistemas de tipo (1) con polinomios de algún grado.
El problema según la lista de Smale
V. I. Arnold, en nombre de la Unión Matemática Internacional, e inspirado en parte por la lista de problemas de Hilbert de 1900 para el siglo XX, propuso a varios matemáticos que elaboraran una nueva lista de problemas para el siglo XXI. Se ha hecho célebre la lista de 18 problemas elaborada por Steve Smale en 1998 (véase [20], que es una traducción de [19]). Según Smale, excepto por la hipótesis de Riemann, la segunda parte del problema 16 parece ser el más difícil de los problemas propuestos por Hilbert. Como problema 13 de su lista, Smale volvió a recoger la segunda parte del problema 16 de Hilbert, pero afinando el enunciado original:
Consideremos la ecuación diferencial polinomial (1) en \(\mathbb{R}^2\). ¿Existe una cota \(K\) de la forma \(K \le d^q\) para el número de ciclos límite, donde \(d\) es el máximo de los grados de \(P\) y \(Q\) y \(q\) es una constante universal?
A partir de ahora, nos preocuparemos sólo por esta versión más moderna de la segunda parte del problema 16 de Hilbert, establecida por Smale en su problema 13.
El propio Smale menciona que el problema general para ecuaciones (1) es demasiado difícil, y que primero deberíamos intentar resolverlo para una clase de ecuaciones diferenciales polinomiales más sencillas. Propuso estudiar el problema restringido a las ecuaciones de Liénard, esto es, a las ecuaciones diferenciales de la forma
$$
\tag{8}
x’ = y – f(x), \quad y’ = -x
$$
donde \(f(x)\) es un polinomio en la variable \(x\) de grado \(d\). El caso \(f(x) = x^3-x\) es una variante de la ecuación de van der Pol que hemos visto en (5) (una ecuación se convierte en la otra utilizando la denominada transformación de Liénard), que tiene un ciclo límite. Incluso en el caso de las ecuaciones de Liénard, no se sabe si hay cotas de la forma \(d^q\) para el número de ciclos límite.
Volviendo al enunciado de Smale con polinomios \(P\) y \(Q\), se llama número de Hilbert para las ecuaciones diferenciales polinomiales de grado \(d\), y se denota \(\mathcal{H}(d)\), al máximo número de ciclos límite en ese caso. Lo que se pretende es identificar \(\mathcal{H}(d)\) para cada \(d\) y probar que \(\mathcal{H}(d) \le d^q\) para cierta constante universal \(q\).
Puesto que las ecuaciones diferenciales polinomiales de grado \(1\) (sistemas diferenciales lineales) no tienen ciclos límite, su número de Hilbert es \(\mathcal{H}(1) = 0\).
Para \(d \ge 2\), no se conoce ninguna cota para el número máximo de ciclos límite que pueden tener las ecuaciones diferenciales polinomiales de grado \(d\). Así que, en principio, para cualquier \(d \ge 2\) podría ocurrir que \(\mathcal{H}(d) = \infty\).
Durante un tiempo se conjeturó que \(\mathcal{H}(2) = 3\), e incluso hubo una demostración que, algo después, se identificó como errónea. Es más, Lan Sun Chen y Ming Shu Wang en 1979 [1] y Song Ling Shi en 1980 [17] proporcionaron ecuaciones diferenciales polinomiales de grado \(d=2\) con \(4\) ciclos límite, lo cual demostraba que \(\mathcal{H}(2) \ge 4\). Actualmente se piensa que, posiblemente, \(\mathcal{H}(2) = 4\), pero no hay seguridad de ello.
Para otros valores de \(d\), no es mucho más lo que se conoce; por ejemplo, se sabe que \(\mathcal{H}(3) \ge 13\) y \(\mathcal{H}(4) \ge 28\). Para \(\mathcal{H}(d)\) en general, el mejor resultado hasta ahora fue probado por Christopher y Lloyd en 1995 [2]; ellos demostraron que \(\mathcal{H}(d)\) crece, al menos, como \(C d^2\log(d)\) para cierta constante \(C > 0\). Y Lloyd conjetura que debe haber una cota superior del número de ciclos de tipo \(O(d^3)\) (en sus propias palabras: «mi razonamiento es simplemente que \(O(d^2)\) puntos críticos pueden ser rodeados por ciclos límite, y que es probable que haya a lo sumo \(O(d)\) ciclos límite alrededor de cada punto crítico»).
Acabamos mencionando que, si llamamos \(\operatorname{Lie}(d)\) al máximo número de ciclos límite para las ecuaciones de Liénard (8) con \(f(x)\) un polinomio de grado \(d\), el problema de conocer \(\operatorname{Lie}(d)\) tampoco está resuelto. Ha habido unas cuantas conjeturas —por ejemplo, durante 40 años se pensó que debería ser \(\operatorname{Lie}(d) \le \lfloor(d-1)/2\rfloor\)— que luego han resultado falsas, y demostraciones que luego han resultado erróneas. Últimamente se han producido pequeños pero importantes avances al respecto, que demuestran que este problema es aún más difícil de lo que parecía. Por ejemplo, se sabe que \(\operatorname{Lie}(d) \ge d-2\) para \(d \ge 6\). Si el lector quiere conocer su estado en el momento de escribir esta nota, puede consular los recientes artículos [7, §2.3] o [8].
Agradecimentos. Agradezco a Armengol Gasull su atenta lectura de varias versiones preliminares de este escrito, y sus sugerencias. Unas cuantas de las descripciones de propiedades o ejemplos que aquí aparecen me las ha proporcionado él.
Referencias
[1] L. S. Chen y M. S. Wang, The relative position, and the number, of limit cycles of a quadratic differential system (en chino, con resumen en inglés), Acta Math. Sinica 22 (1979), 751–758.
[2] C. J. Christopher y N. G. Lloyd, Polynomial systems: A lower bound for the Hilbert numbers, Proc. Roy. Soc. London Ser. A 450 (1995), 219–224.
[3] C. S. Coleman, Hilbert’s 16th problem: How many cycles?, Differential Equation Models, Modules in Applied Mathematics, Vol. 1, 279–297, Springer-Verlag, 1983.
[4] H. Dulac, Sur les cycles limites, Bull. Soc. Math. France 51 (1923), 45–188.
[5] J. Écalle, Introduction aux fonctions analysables et preuve constructive de la conjecture de Dulac, Hermann, 1992.
[6] A. Gasull, De les equacions diferencials d’Abel al problema XVI de Hilbert, Butl. Soc. Catalana Mat. 28 (2013), 123–146.
[7] A. Gasull, Some open problems in low dimensional dynamical systems, SeMA Journal 78 (2021), 233–269.
[8] A. Gasull, From Abel’s differential equations to Hilbert’s 16th problem, São Paulo J. Math. Sci., número especial «Stability and Bifurcation – Memorial Issue Dedicated to Jorge Sotomayor», por aparecer, 2024.
[9] A. Gasull, H. Giacomini y J. Torregrosa, Explicit non-algebraic limit cycles for polynomial systems, J. Comput. Appl. Math. 200 (2007), 448–457.
[10] A. Gasull, A. Guillamon y V. Mañosa, Counting configurations of limit cycles and centers, Bul. Acad. Ştiinţe Repub. Mold. Mat. 101 (2023), no. 1, 78–96.
[11] Y. Ilyashenko, Dulac’s memoir “On limit cycles” and related problems of the local theory of differential equations, Russian Math. Surveys 40 (1985), 1–49.
[12] Y. Ilyashenko, Finiteness theorems for limit cycles, Translations of Math. Monographs, 94, American Mathematical Society, 1991.
[13] J. Llibre, Sobre el problema 16 de Hilbert, La Gaceta de la RSME 18 (2015), 543–554.
[14] J. Llibre y G. Rodríguez, Configurations of limit cycles and planar polynomial vector fields, J. Differential Equations 198 (2004), 374–380.
[15] J. Llibre y Y. Zhao, Algebraic limit cycles in polynomial systems of differential equations, J. Phys. A 40 (2007), 14207–14222.
[16] K. Odani, The limit cycle of the van der Pol equation is not algebraic, J. Differential Equations 115 (1995), 146–152.
[17] S. L. Shi, A concrete example of the existence of four limit cycles for plane quadratic systems, Sci. Sinica 23 (1980), 153–158.
[18] F. Simmons, Ecuaciones diferenciales con aplicaciones y notas históricas, MacGraw-Hill, 1972.
[19] S. Smale, Mathematical problems for the next century, Math. Intelligencer 20 (1998), no. 2, 7–15.
[20] S. Smale, Problemas matemáticos para el próximo siglo, La Gaceta de la RSME 3 (2000), 413–434.

Dejar una contestacion