En la entrada anterior comentamos la famosa paradoja EPR, que nos condujo a la pregunta de si la mecánica cuántica era una teoría completa o no, y lo que era incluso más importante, como confirmarlo experimentalmente. En esta entrada nos ocuparemos de esta cuestión.
Nuestro protagonista será el físico norirlandés John Stewart Bell. Antes de explicar su maravillosa idea conviene dar unas pinceladas biográficas.
John Stewart Bell nació en Belfast el 28 de julio de 1928. Su madre provenía una familia acomodada que lo perdió todo en un incendio a principios del siglo XX y su padre provenía de una familia cuidadora de caballos. Desde los 11 años John decidió que iba a estudiar ciencias aunque tuvo que trabajar desde los 12 para ayudar a su familia. Afortunadamente consiguió una beca para estudiar en la Belfast Technical High School graduándose con 16 años en 1944. Aunque su intención era estudiar física en la Queen’s University de Belfast tenía un par de pequeños problemas: la edad mínima de admisión era 17 años y, como ya mencionamos, tenía que trabajar para ayudar a su familia.

Afortunadamente para todos consiguió una plaza de ayudante de laboratorio en el Departamento de Física del la Queen’s University bajo la supervisión del profesor Karl Emeleus, en ese momento director del Departamento. Tras un año Emeleus le consiguió una beca que le permitió el acceso a la Universidad y pudo licenciarse (con honores) en el grado de Física experimental en 1948 y, un año más tarde en 1949, en Física-matemática. Ese último año fue providencial para el joven físico pues fue acogido por el famoso cristalógrafo Paul Peter Ewald (refugiado alemán, que sin ser judío fue expulsado de la Universidad de Stuttgart, de la que había sido rector hasta 1933, por sus desavenencias con el régimen nazi -protestó por la expulsión de los profesores judíos de la Universidad- lo que le permitió profundizar en las bases de la Mecánica cuántica, una teoría que este conocía de primera mano. Ewald era un reconocido físico (teórico y experimental) alemán que durante 1913 trabajó, recomendado por Sommerfeld (del cual fue alumno), como asistente de Hilbert en las cuestiones de la Física en Gotinga. Con Ewald, Bell se familiarizó con las bases de la Mecánica cuántica y aunque hubiese querido continuar sus estudios haciendo un doctorado, decidió que tenía que ayudar a su familia y se puso a buscar trabajo.
Gracias al apoyo que le brindaron tanto Emeleus como Ewald, John consiguió un puesto en el Atomic Energy Research Establishment, que era principal centro de investigación y desarrollo de energía atómica del Inglaterra, en la ciudad de Harwell en 1949. En Harvell trabajó brevemente en el departamento liderado por Klaus Fuchs, el famoso físico teórico y miembro del proyecto Manhattan que participó activamente en la construcción de la primera bomba atómica de plutonio, y que pasó la información a los servicios secretos de la Unión Soviética. Tras el arresto de Fuchs en febrero de 1950 (por los cargos de espionaje) Bell fue transferido a Malvern para trabajar en el diseño de un acelerador de partículas. Fue allí donde conoció a la que sería su esposa Mary Ross una talentosa física y matemática que era parte del mismo equipo que Bell y con quien se casó en 1954 tras regresar de disfrutar un año sabático en la Universidad de Birmingham donde defendió su tesis doctoral bajo la dirección de Rudolf Peierls (también participante en el proyecto Manhattan junto a Fuchs). En 1960 al cerrar los departamentos donde trabajaba la joven pareja, estos renunciaron a su puesto fijo en Harvell y se mudaron al recién nacido CERN (Conseil Européen pour la Recherche) en Ginebra donde residieron hasta la repentina muerte de Bell en 1990 de un derrame cerebral. En el CERN el trabajo de Bell se centró en la física de partículas, la física nuclear, y como no, en las bases de la Mecánica cuántica. Si en las dos primeras disciplinas hizo contribuciones relevantes, fue la tercera (a la que solía llamar su hobby) la que le llevó a la fama.
Pero volvamos al problema de la completitud de la Mecánica cuántica. La historia, contada muy escuetamente es como sigue. Bell se interesó por el problema de las variables ocultas tras leer los dos trabajos de Bohm A suggested interpretation of quantum theory in terms of ‘hidden’ variables I y II publicados en 1952 en la prestigiosa Physical Review. En ellos Bohm construía una mecánica cuántica de variables ocultas lo cual, aparentemente, era imposible según un resultado de von Neumann de su famoso tratado de 1932 (del que ya hablamos AQUÍ). Pues bien, Bell probó en un artículo titulado On the problem of hidden variables in quantum mechanics publicado en Review of Modern Physics en 1966, que el resultado de von Newmann (luego generalizado por otros) tenía un fallo cuando afirmaba que los resultados experimentales de la Mecánica cuántica no podían derivarse de una teoría de variables ocultas (von Newmann eligió una hipótesis de partida que, desde el punto de vista físico, no era del todo correcta). El trabajo de Bell no solo era matemáticamente impecable sino que al final del mismo se sugería que quizá las teorías de variables ocultas podrían ser no locales (para una explicación sobre el concepto de localidad ver la entrada anterior). En un segundo trabajo (aunque publicado antes del anterior, cosas del mundo académico) titulado On the Einstein Podolsky Rosen paradox publicado en 1964 Bell, que era partidario de Einstein más que de Bohr (ver la entrada anterior para ese respecto), se preguntaba si podría haber alguna teoría local de variables ocultas.
Para resolver el problema lo que hizo Bell fue hacerse la pregunta contraria: Si las propiedades son reales y locales, ¿qué consecuencias experimentales tiene eso? Y consiguió dar con una idea brillante, algo que debería haberle valido un premio Nobel (de hecho fue propuesto para el Nobel en 1990, el mismo año que murió de una hemorragia cerebral). Así, Bell descubrió una expresión matemática muy sencilla que debía cumplirse si una teoría era local-realista y mostró que la Mecánica cuántica no la cumplía. Además sugirió un posible experimento para comprobarlo experimentalmente. Y ¿cuál era esa expresión matemática? Pues una desigualdad muy sencilla.

Por simplicidad vamos a mostrar una versión más sencilla de la desigualdad de Bell debida a Clauser, Horne, Shimony y Holt conocida como la desigualdad CHSH y publicada en un artículo titulado Proposed Experiment to Test Local Hidden-Variable Theories aparecido en Physical Review Letters en 1970.
Para ello realizaremos el siguiente experimento mental donde participarán otra vez Alice, Bob y Charlie.
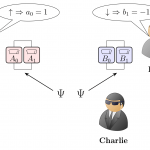
Supongamos que Charlie, el amigo de Alice y Bob, prepara un número de pares de partículas iguales (en el mismo estado \(\Psi\)) y le envía una a Alice y la otra a Bob. Cuando Alice recibe la suya decide hacer una de dos posibles mediciones \(A_0\) y \(A_1\) y obtiene como resultado el valor \(a_0=1\) o \(-1\) para \(A_0\) y \(a_1=1\) o \(-1\) para \(A_1\). Análogamente Bob puede hacer dos mediciones \(B_0\) y \(B_1\) cuyos resultados son \(b_0=1\) o \(-1\) para \(B_0\) y \(b_1=1\) o \(-1\) para \(B_1\). Supongamos además que el resultado de la medición es una propiedad real de la partícula, por ejemplo que los valores de \(a_0=1\) o \(-1\) corresponden al espín \(\uparrow\) o \(\downarrow\), respectivamente (y lo mismo para Bob) y no cambian al hacer las mediciones (teoría realista). Supongamos además que el experimento se hace de forma que Alice y Bob hacen la medición al mismo tiempo, es decir, la medición Alice no puede influir en el resultado de la medición de Bob (teoría local).
Calculemos el valor de la siguiente cantidad
$$
M=a_0b_0+a_0b_1+a_1b_0-a_1b_1=(a_0+a_1)b_0+(a_0-a_1)b_1.
$$
Como \(a_0\) y \(a_1\) toman los valores \(\pm1\), entonces siempre tendremos que \(a_0=a_1\) o que \(a_0=-a_1\), y por tanto \(M\) solo puede tomar los valores \(M=\pm2\).
Supongamos ahora que \(p(a_0,a_1,b_0,b_1)\) es la probabilidad de que antes de que Alice y Bob hagan sus mediciones el sistema esté en el estado \((a_0,a_1,b_0,b_1)\), es decir, que el valor de \(A_0\) es \(a_0\), el de \(A_1\) es \(a_1\), el de \(B_0\) es \(b_0\) y el de \(B_1\) es \(b_1\). Dicha probabilidad puede depender de muchas variables (incluso de variables ocultas) aparte de las que estamos midiendo. En cualquier caso la media de \(M\), que denotaremos por \(\langle M\rangle\) es
$$\small\langle M\rangle=\sum_{a_i,b_i} p(a_0,a_1,b_0,b_1) [a_0b_0+a_0b_1+a_1b_0-a_1b_1]=\langle A_0B_0\rangle+ \langle A_0B_1\rangle+ \langle A_1B_0\rangle- \langle A_1B_1\rangle,$$ donde la suma recorre todos los posibles valores de \(a_0,a_1,b_0,b_1\). De la fórmula anterior se deduce la siguiente desigualdad de Bell:
$$|\langle M\rangle|=|\langle A_0B_0\rangle+ \langle A_0B_1\rangle+ \langle A_1B_0\rangle- \langle A_1B_1\rangle |\leq 2.$$
Es decir, si una teoría es realista y local el valor medio de \(M\) tras realizar un gran número de mediciones por parte de Alice y Bob no puede ser mayor, en valor absoluto, que dos. Por tanto, en el mundo local-realista obtendremos desigualdad
$$|\langle M\rangle|\leq2.$$
Nótese que Alice y Bob pueden estimar el valor de \(\langle M\rangle\) simplemente repitiendo el experimento una gran número de veces y apuntando cada una de las veces los valores medidos por cada uno. Luego Alice y Bob se juntan e intercambian la información. Por ejemplo, ambos miran los resultados de los experimentos cuando Alice midió \(A_0\) y Bob \(B_1\) y hacen la media de los valores de \(a_0b_1\) obtenidos, y así con cada una de los productos \(a_0b_0\), \(a_1b_0\) y \(a_1b_1\). Mientras más observaciones hayan hecho más precisas serán las medias de los correspondientes productos.
¿Qué dice la Mecánica cuántica? Para responder a esa pregunta necesitamos un poquito de matemáticas.
Supongamos que las partículas que enviamos a Alice y a Bob son dos partículas entrelazadas en el estado
$$
\Psi=\frac{1}{\sqrt{2}}|\!\uparrow \rangle_A \otimes |\!\downarrow \rangle_B -\frac{1}{\sqrt{2}}|\!\downarrow \rangle_A\otimes|\!\uparrow \rangle_B.
$$
donde los estados espín up \(|\!\uparrow\rangle\) y espín down \(|\!\downarrow \rangle\) son los autovalores del operador \(\sigma_z\) que tiene asociado la matriz de Pauli correspondiente a la proyección del espín en el eje \(z\). Sea el operador \(\sigma_x\) el operador cuya matriz es la matriz de Pauli asociada a la proyección del espín en el eje \(x\). Para dichos operadores se tiene que
$$
\sigma_z |\!\uparrow\rangle= |\!\uparrow\rangle ,\quad
\sigma_z |\!\downarrow\rangle \ =-|\!\downarrow\rangle \quad
\sigma_x |\!\uparrow\rangle=|\!\downarrow\rangle, \quad
\sigma_x |\!\downarrow\rangle= |\!\uparrow \rangle
$$
Supongamos que Alice decide las cantidades \(A_0=\sigma_z\) y \(A_0=\sigma_x\) y Bob
$$
B_0=-\frac{\sigma_x+\sigma_z}{\sqrt{2}},\quad \mbox{y} \quad B_1=\frac{\sigma_x-\sigma_z}{\sqrt{2}}.
$$
Ahora bien, en la mecánica cuántica las mediciones de Alice y Bob son independientes así que para calcular la media \(\langle A_iB_j\rangle\), \(i=0,1\), tenemos que usar la regla de Born:
$$
\langle A_iB_j\rangle= \langle \Psi | A_i\otimes B_j |\Psi\rangle,
$$
y que tener en cuenta que \(A_i\) actúa solamente sobre los estados \(|\!\uparrow \rangle_A\) y \(|\!\downarrow \rangle_A\) y los \(B_j\) sobre los \(|\!\uparrow \rangle_B\) y \(|\!\downarrow \rangle_B\). Tras las correspondientes cuentas (que el lector interesado puede encontrar en el apéndice de la entrada) se obtiene
$$\langle \Psi |A_0 B_0|\Psi\rangle = \frac1{\sqrt{2}}, \quad \langle \Psi |A_0 B_1|\Psi\rangle = \frac1{\sqrt{2}},\quad
\langle \Psi |A_1 B_0|\Psi\rangle = \frac1{\sqrt{2}},\quad
\langle \Psi |A_1 B_1|\Psi\rangle = -\frac1{\sqrt{2}}$$
y, por tanto,
$$
|\langle M\rangle|=|\langle A_0B_0\rangle+ \langle A_0B_1\rangle+ \langle A_1B_0\rangle- \langle A_1B_1\rangle |=2\sqrt{2}>2,
$$
lo cual contradice la desigualdad de Bell que vimos antes.

Es conveniente aclarar que lo que acabamos de probar, es decir, que se viola la desigualdad de Bell, no dice que la mecánica cuántica esté mal y tampoco implica que sea una teoría incompleta, lo que nos dice es que no puede ser una teoría local-realista: o es local, o es realista (en el sentido que explicamos en la entrada anterior), o ninguna de las dos. Sin embargo el avispado lector se habrá dado cuenta de una cosa obvia: todo lo que hemos contado hasta aquí es puramente teórico. La desigualdad de Bell tanto en la forma CHSH, como en la original del propio Bell, es una cuenta teórica y el cálculo cuántico de la media de \(M\) también lo es. Para saber cómo es el mundo que nos rodea tenemos que mirar en él, o sea, ver si es posible confirmar la desigualdad de Bell o no experimentalmente.
Si bien en su artículo antes citado de 1968 Clauser, Horne, Shimony, and Holt (CHSH) propusieron un experimento con fotones polarizados para verificar la desigualdad de Bell, los primeros en realizar el experimento para probar experimentalmente que la mecánica cuántica no cumplía la desigualdad de Bell fueron Freedman y Clauser (el mismo de CHSH) en 1972. Sin embargo, fue el físico francés Aspect con su equipo de la Universidad d’Orsay (actualmente Universidad Paris-Sud) los que en 1982 realizaron una serie de experimentos que mostraron, sin la más mínima duda, que la cuántica no cumplía la desigualdad de Bell. Por los experimentos con fotones entrelazados, estableciendo la violación de las desigualdades de Bell John Clauser y Alain Aspect recibieron en el 2022 el premio Nobel de física que compartieron con Anton Zeilinger, este último por sus trabajos pioneros en la ciencia de la información cuántica, así que al final la contribución de Bell si recibió el mérito que merecía.
Antes de terminar conviene remarcar lo que no dice el Teorema de Bell. Para ello tomaremos prestadas las palabras escritas por Pedro Gómez-Esteban González en su fabuloso blog eltamiz.com
Hay otra cosa que tampoco dice el Teorema de Bell, aunque a veces se oiga por ahí. No dice que si se incumple la desigualdad «la cuántica tiene razón». Es perfectamente posible que haya una teoría más completa, mejor, más precisa que la cuántica […] pero, lo que quiera que sea que la reemplace, no puede ser una teoría local-realista. En otras palabras: la cuántica es rara, y tal vez esté equivocada, pero no es rara por estar equivocada; cualquier teoría que la reemplace también será rara, porque el Universo lo es.
Como colofón recordemos la famosa carta de Einstein a Born del 7 de septiembre de 1944 donde este le escribía
Nos hemos convertido en antípodas en relación a nuestras expectativas científicas. Tú crees en un Dios que juega a los dados, y yo, en la ley y el orden absolutos en un mundo que existe objetivamente […]. Ni siquiera el gran éxito inicial de la teoría cuántica me hace creer en un juego de dados fundamental […]. Sin duda llegará el día en que veremos de quién fue la actitud instintiva correcta.
Desgraciadamente para Einstein, Born tenía razón: Dios, definitivamente, juega a los dados.
Para saber más:
\(\bullet\) Bell escribió en 1987 un librito imprescindible titulado Speakable and Unspeakable in Quantum Mechanics, Cambridge University Press, (ampliado en 2004 con dos artículos extra y una introducción por Alain Aspect) que contiene los dos trabajos fundamentales de Bell aquí descritos junto con una serie de interesantes trabajos bajo el título «Artículos sobre filosofía cuántica».
\(\bullet\) El experimento de CHSH está muy bien descrito en el apartado 2.6 (páginas 111-117) del libro M.A. Nielsen y I.L. Chuang, Quantum Computation and Quantum Information. 10th Anniversary Edition (2011, Cambridge University Press)
\(\bullet\) El experimento más famoso quizá es el que describe N.D. Mermin en 1985 en su ensayo Is the Moon There When Nobody Looks? Reality and the Quantum Theory. Phys. Today 38(4), 38 (1985)
y que luego reescribe de forma magistral con sus cuantejos Pedro Gómez-Esteban en el ya mencionado blog eltamiz.
\(\bullet\) Pedro Gómez-Esteban González, El teorema de Bell.
La imagen destacada es una superposición de la imagen de luz visible más profunda del cosmos, el Campo Ultra Profundo del Hubble y los dados de Dios.
Anexo para los más matemáticos: El cálculo de las medias
Para calcular la media \(\langle A_iB_j\rangle\), \(i=0,1\), usamos la regla de Born:
$$
\langle A_iB_j\rangle= \langle \Psi | A_i\otimes B_j |\Psi\rangle,\quad \Psi:=\Psi=\frac{1}{\sqrt{2}}|\!\uparrow \rangle_A \otimes |\!\downarrow \rangle_B -\frac{1}{\sqrt{2}}|\!\downarrow \rangle_A\otimes|\!\uparrow \rangle_B.
$$
Para ello hay que tener en cuenta que el operador \(A_i\) actúa solamente sobre los estados \(|\!\uparrow \rangle_A\) y \(|\!\downarrow \rangle_A\) y los \(B_j\) sobre los \(|\!\uparrow \rangle_B\) y \(|\!\downarrow \rangle_B\). Así
$$
A_i\otimes B_j \bigg( |\!\uparrow \rangle_A \otimes |\!\downarrow \rangle_B \bigg)
= A_i |\!\uparrow \rangle_A \otimes B_j |\!\downarrow \rangle_B.
$$
Luego, por ejemplo,
$$
\bigg( {}_A\langle\uparrow\!| \otimes {}_B\langle \downarrow\!| \bigg) A_i\otimes B_j \bigg( |\!\uparrow \rangle_A \otimes |\!\downarrow \rangle_B \bigg)=
\langle\uparrow\!| A_i |\!\uparrow \rangle_A \langle \downarrow\!|B_j |\!\downarrow \rangle_B.
$$
En adelante por comodidad eliminaremos el símbolo \(\otimes\) y los subíndices \(A\) y \(B\) recordando la regla anterior. Para evitar confusiones denotaremos por \(\sigma\) los operadores espín que actúan sobre los estados \(A\) y por \(\hat{\sigma}\) los que actúan sobre \(B\), respectivamente. Además, usaremos la notación \(|\!\!\uparrow \downarrow\rangle:=|\!\!\uparrow \rangle_A \otimes |\!\!\downarrow \rangle_B\) y \(|\!\downarrow\uparrow\rangle:=|\!\downarrow \rangle_A\otimes|\!\uparrow \rangle_B\).
Calculemos el valor \(\langle \Psi |A_0 B_0|\Psi\rangle\)
\begin{align*}
\langle \Psi |A_0 B_0|\Psi\rangle =& -\frac1{\sqrt{2}}\left[
\langle \Psi |\sigma_z \hat{\sigma}_x |\Psi\rangle+\langle \Psi |\sigma_z \hat{\sigma}_z |\Psi\rangle\right] \\ &
-\frac1{2\sqrt{2}}\bigg(\langle\uparrow \downarrow\!| – \langle \uparrow \downarrow \!| \bigg) \sigma_z \hat{\sigma}_x \bigg( |\!\!\uparrow \downarrow\rangle- |\!\downarrow\uparrow\rangle \bigg) \\
= &
-\frac1{2\sqrt{2}}\bigg(
\langle\uparrow \downarrow\!| \sigma_z \hat{\sigma}_x |\!\!\uparrow \downarrow\rangle+
\langle\uparrow \downarrow\!| \sigma_z \hat{\sigma}_z |\!\!\uparrow \downarrow\rangle-
\langle\uparrow \downarrow\!| \sigma_z \hat{\sigma}_x |\!\! \downarrow\uparrow\rangle-
\langle\uparrow \downarrow\!| \sigma_z \hat{\sigma}_z |\!\! \downarrow\uparrow\rangle\\ &
\qquad\quad-
\langle \downarrow\uparrow\!| \sigma_z \hat{\sigma}_x |\!\!\uparrow \downarrow\rangle-
\langle \downarrow\uparrow\!| \sigma_z \hat{\sigma}_z |\!\!\uparrow \downarrow\rangle
+\langle \downarrow\uparrow\!| \sigma_z \hat{\sigma}_x |\!\! \downarrow\uparrow\rangle+
\langle \downarrow\uparrow\!| \sigma_z \hat{\sigma}_z |\!\! \downarrow\uparrow\rangle
\bigg)\\
= &
-\frac1{2\sqrt{2}}\bigg(
{\langle\uparrow \downarrow\!| \!\!\uparrow \uparrow\rangle}-
{\langle\uparrow \downarrow\!| \!\!\uparrow \downarrow\rangle}-
{\langle\uparrow \downarrow\!| \!\! \downarrow\downarrow\rangle}+
{\langle\uparrow \downarrow\!| \!\! \downarrow\uparrow\rangle}-
{\langle \downarrow\uparrow\!| \!\!\uparrow \uparrow\rangle}+
{\langle \downarrow\uparrow\!| \!\!\uparrow \downarrow\rangle}\\ &
\qquad-
{\langle \downarrow\uparrow\!| \!\! \downarrow\downarrow\rangle}-
{\langle \downarrow\uparrow\!| \!\! \downarrow\uparrow\rangle}
\bigg)=-\frac1{2\sqrt{2}}\bigg(0-1-0+0-0+0-0-1\bigg)=\frac1{\sqrt{2}},
\end{align*}
donde hemos usado, por un lado las fórmulas para los operadores espín y, por el otro, que los estados \(|\!\!\uparrow \rangle\) y \(|\!\!\downarrow\rangle\) son ortonormales entre sí. De forma análoga se prueban el resto de las medias.

Dejar una contestacion