La meteorología, palabra que según la Wikipedia proviene del griego meteoro que significa alto en el cielo y lógos que significa conocimiento, es, según el diccionario de la RAE, la Ciencia que estudia los fenómenos atmosféricos. Uno de sus principales propósitos es la previsión del tiempo. La meteorología tiene su origen en la antigüedad siendo Aristóteles uno de los primeros en interesarse en su estudio tal y como se recoge en su monumental obra Meteorológicos. Existen dos ramas bien diferenciadas de meteorología. Por un lado está la meteorología sinóptica que estudia los fenómenos meteorológicos en tiempo real, basándose en las observaciones realizadas a la misma hora y anotadas sobre mapas geográficos con el objeto de predecir el estado del tiempo futuro. Un ejemplo típico es el mapa de presiones que solemos ver en la tele. Un ejemplo es el siguiente mapa de presión:
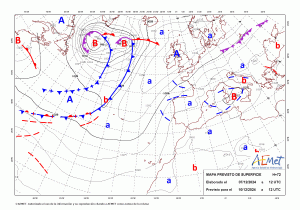
La meteorología sinóptica era la forma habitual y hasta hace relativamente poco la única que se usaba y se basa, en parte, en la intuición del meteorólogo. En muchos sentidos era más un arte que una ciencia. Por otro lado tenemos la meteorología dinámica que consiste en modelar los movimientos atmosféricos mediante sistemas de ecuaciones diferenciales que se deducen a partir de las leyes de la hidrodinámica (la atmósfera es un fluido) y la termodinámica. En este caso está claro que las técnicas de modelización matemática así como los métodos numéricos son esenciales. Conviene recalcar que en ambos casos es de enorme importancia disponer de datos fiables de variables meteorológicas como la temperatura, velocidad del viento, humedad, presión, etc, que son recolectados en las estaciones meteorológicas, mediante satélites, etc. Sin ellos es imposible hacer cualquier tipo de pronóstico.
En esta entrada nos centraremos en la meteorología dinámica. Los modelos actuales de la dinámica atmosférica tienen una ingente cantidad de variables y las matemáticas necesarias para entenderlos van mucho más allá de lo que se puede explicar en una entrada como esta. Basta decir que se basan, entre otras, en las ecuaciones de la dinámica de fluidos, entre las cuales están las ecuaciones de Navier-Stokes, famosas por ser uno de los siete problemas matemáticos cuya resolución sería premiada por el Clay Mathematics Institute con un millón de dólares cada uno (y de las que ya se habló aquí y aquí).
A efectos prácticos, y dada la imposibilidad de resolver las ecuaciones que modelan la dinámica atmosférica de forma analítica, lo que se hace es resolverlas numéricamente, siendo el matemático y meteorólogo Lewis F. Richardson el primero en describir un tratado sobre el tema (ver Weather prediction by numerical process publicado en 1922, mucho antes de que aparecieran los ordenadores modernos).

En esta entrada vamos a describir un modelo mucho más sencillo debido a Edward N. Lorenz en 1963 que no solo revolucionó la meteorología, sino también las propias matemáticas y es suficiente para mostrar la imposibilidad práctica de predecir el tiempo a largo plazo, algo que parece no entienden algunas asociaciones que tras la desastrosa DANA del pasado 29 de octubre de 2024 en España llegaron a denunciar a la AEMET por presuntos delitos de homicidio por imprudencia, lesiones y daños.
La intención de Lorenz era modelar el movimiento convectivo (es decir el movimiento de las partes calentadas de un líquido o gas) de una celda de un fluido bidimensional que se calienta desde abajo y se enfría desde arriba. Con dicho modelo Lorenz pretendía entender como podía evolucionar una región de la atmósfera comprendida entre dos masas de aire de diferentes temperaturas. Su trabajo estaba motivado por un trabajo de Barry Saltzman de 1962 donde se reducían las ecuaciones que modelan los procesos de convección térmica de un fluido usando la aproximación de Oberbeck–Boussinesq a un sistema de dos ecuaciones en derivadas parciales no lineales.
El sistema obtenido es imposible de resolver analíticamente así que tanto Saltzman como Lorenz usaron un método aproximado para intentar estudiarlo. La idea consistía en usar un desarrollo apropiado en series de Fourier (de las que ya hablamos aquí). En el caso de Lorenz, este llegó al sistema de tres ecuaciones con tres incógnitas que tenemos a continuación:
$$ \dfrac{dx}{dt} = \delta [y(t) – x(t))],\quad \dfrac{dy}{dt} = r x(t) – y(t) – x(t) z(t),\quad
\dfrac{dz}{dt} = x(t) y(t) – b z(t). \quad (*)
$$
En el modelo la función \(x(t)\) representa intensidad del movimiento convectivo, mientras que \(y(t)\) y \(z(t)\) están relacionadas con la variación de temperatura horizontal y vertical, respectivamente. Los números \(\delta\), \(r\) y \(b\) que aparecen dependen de ciertas constantes termodinámicas y de mecánica de fluidos y lo relevante es que son positivas. Para poder predecir los valores de \(x(t)\), \(y(t)\) y \(z(t)\) hay que conocer los valores de dichas cantidades en un determinado momento de tiempo, digamos \(t_0=0\).
Lorenz, se puso manos a la obra para resolver su sistema numéricamente. Eso hubiese sido impensable algunos años antes. Solo con la aparición de los primeros computadores electrónicos el sueño de poder realizar miles de cálculos matemáticos en pocos segundos se hizo realidad y eso ocurrió después de terminada la Segunda Guerra Mundial. Así que Lorenz, que disponía de un ordenador de sobremesa (un Royal McBee LGP-30 que era el PC de aquel tiempo, aunque sus dimensiones eran 84 por 112 por 66 cm y su peso 360 Kg), escribió un programa para la resolución del sistema de ecuaciones y se propuso ver cómo evolucionaba su modelo simplificado de predicción del tiempo.
La idea de Lorenz era una idea muy clásica, muy newtoniana: usando las leyes físicas conocidas obtener un sistema de ecuaciones que describiera, dentro de ciertos límites, la realidad. Esa era la filosofía imperante hasta ese momento: dado que se partía de ecuaciones deterministas, el resultado sería un modelo determinista. El mejor ejemplo se tenía con los modelos astronómicos. Los astrónomos, aunque eran conscientes de que era imposible resolver el problema del movimiento planetario si se tenían en cuenta todos los planetas, satélites y asteroides del sistema solar, eran capaces de predecir con una tremenda precisión las órbitas de los planetas, la órbita de un cometa (como el Halley), las órbitas de satélites artificiales y la de los misiles intercontinentales. ¿Por qué no iba a funcionar igual la predicción del tiempo? Al fin y al cabo las ecuaciones seguían siendo deterministas ¿o no?
Al margen de lo anterior, había también una especie de creencia generalizada de que si se conocían las condiciones de partida de un sistema determinista con suficiente precisión, entonces las predicciones obtenidas tras su resolución serían razonablemente precisas. H. Poincaré en su Ciencia y Método publicado en 1914 lo expresaba con estas palabras:
Una causa muy pequeña que escapa a nuestra atención determina un efecto considerable que no podemos dejar de ver, y entonces decimos que tal efecto se debe a la casualidad. Si conociésemos de manera exacta las leyes de la naturaleza y la situación del Universo en el momento inicial, podríamos predecir -igualmente de manera exacta- la situación de tal Universo en un momento subsecuente. Pero, incluso si fuese tal caso, sólo podríamos conocer la situación inicial de manera aproximada. Si eso nos permitiese predecir la situación subsecuente con la misma aproximación, sería todo lo que necesitamos, y podríamos decir que el fenómeno ha sido predicho, y que está gobernado por ciertas leyes.
En su maravilloso libro Caos: La creación de una ciencia, James Gleick nos actualiza la cita de Poincaré de esta forma (entre corchetes comentarios del que esto escribe)
Esta presunción ocupa el corazón filosófico de la ciencia. Como un teórico [A.T. Winfree] tenía la afición de decir a sus alumnos: «La idea básica de la ciencia occidental es que no debemos considerar la caída de una hoja de un planeta de otra galaxia cuando queremos explicar el movimiento de una bola en una mesa de billar de la Tierra. Puede prescindirse de las influencias mínimas. Hay una convergencia en el modo como ocurren las cosas, y pequeñas influencias arbitrarias no se amplifican hasta tener grandes efectos arbitrarios.» Desde el punto de vista clásico, estaba bien justificada la creencia en la aproximación y la convergencia. Era eficaz. Un error nimio en fijar la posición del cometa Halley en 1910 causaría sólo un minúsculo error al predecir su llegada en 1986, error que continuaría siendo insignificante en el futuro durante millones de años. Los ordenadores [simulaciones numéricas] se basan en el mismo supuesto para guiar naves espaciales: una entrada (input) aproximadamente precisa da como resultado una salida (output) aproximadamente precisa. Los pronosticadores económicos se basan en este supuesto, aunque su éxito es menos evidente. Lo mismo hicieron los pioneros en la predicción meteorológica global.
Y Edward Lorenz era, sin duda, uno de esos pioneros. Ahora bien, el uso de los ordenadores para predecir el tiempo debe sin duda mucho a von Neumann (de quién ya hemos hablado en varias ocasiones en este blog, por ejemplo aquí) pues este, a pesar de no ser formalmente meteorólogo, era consciente de que un buen test para las flamantes nuevas máquinas que él había ayudado a crear era precisamente su uso para resolver el problema, nada trivial, de la predicción del tiempo. El propio Lorenz en un ilustrador libro titulado The essence of Chaos (publicado por primera vez en 1990) describe el nacimiento de la meteorología dinámica por ordenador que, según él, es la esencia del uso de modelos dinámicos para la predicción del tiempo. En dicho texto Lorenz nos cuenta, por ejemplo, como era el modelo utilizado por la ECMWF (European Centre for Medium-Range Weather Forecasts) con sede en Reading, Reino Unido en 1991.
El modelo en sí es global y, como la mayoría de los grandes modelos actuales, se basa en ecuaciones primitivas [ecuaciones lo más realistas posibles]. […] En 1985, poseía tres magnitudes físicas (temperatura y dos componentes del viento) definidas en cada una de las diecinueve elevaciones [secciones verticales de aire] […], y una cuarta magnitud (contenido de vapor de agua) […]. La presión se definió explícitamente sólo en el nivel más bajo, ya que las presiones en los niveles superiores podían inferirse de las de los niveles inferiores cuando se conocían las temperaturas y humedades en los niveles intermedios. Se definieron otras variables auxiliares, como la humedad del suelo, cuando correspondía. Cada magnitud física en cada nivel se especificó, a efectos prácticos, en una cuadrícula de más de 11.000 puntos que abarcaba todo el globo. Esto produjo un total de unas 800.000 variables. Como si esto no fuera suficiente, a finales de 1991 se duplicó la resolución tanto en dirección latitudinal como longitudinal, produciendo 45.000 puntos de cuadrícula, mientras que el número de elevaciones estándar se incrementó a 31. Esto produjo un modelo con cinco millones de variables. De este material se hacen los modelos de circulación global modernos.
Imáginese el lector cuántas variables puede tener hoy ese modelo. Si tiene curiosidad por ver el modelo actual puede visitar la web del ECMWF y concretamente descargar los informes del Integrated Forecasting System. Por razones obvias no vamos a explicar aquí un modelo tan sofisticado. Ni siquiera vamos a describir el modelo de doce variables original que usó Lorenz en 1961. Lo que haremos es recuperar el modelo simplificado de Lorenz con el que comenzamos esta entrada, pues dicho modelo nos permitirá, de forma sencilla, mostrar lo que descubrió Lorenz con su modelo numérico original y que ejemplifica la imposibilidad de la previsión del tiempo a largo plazo. Dejemos que nos lo cuente el propio Lorenz
En un momento dado, decidí repetir algunos de los cálculos para examinar con más detalle lo que estaba sucediendo. Detuve la computadora, escribí la línea de números que había impreso un rato antes y la puse en funcionamiento nuevamente. Fui al pasillo a tomar una taza de café y regresé después de aproximadamente una hora, durante la cual la computadora había simulado el clima de aproximadamente dos meses. Los números que se imprimían no se parecían en nada a los antiguos.
Aunque al principio Lorenz no se dio cuenta de lo que ocurría (pensó que era un problema de su ordenador), tras repetir varias veces las simulaciones y analizar los resultados Lorenz concluyó que no había ningún error. Así continua Lorenz su historia (recuérdese que Lorenz estaba modelando el tiempo atmosférico en tiempo real)
En lugar de una ruptura repentina, descubrí que los nuevos valores al principio repetían los antiguos, pero poco después diferían en una y luego en varias unidades en el último decimal, y luego empezaron a diferir en el penúltimo decimal y luego en el anterior. De hecho, las diferencias se duplicaron de forma más o menos constante cada cuatro días aproximadamente, hasta que toda semejanza con el resultado original desapareció en algún momento del segundo mes. Esto fue suficiente para decirme lo que había sucedido: los números que había escrito no eran exactamente los números originales, sino los valores redondeados que habían aparecido en la impresión original. Los errores iniciales de redondeo eran los culpables; se fueron amplificando de manera constante hasta que dominaron la solución. En la terminología actual, había caos.
Veamos con algo más de detalle lo que encontró Lorenz al regresar de su café. Para ello usaremos el sistema de ecuaciones (*). Fijemos en las ecuaciones del sistema (*) los valores
$$
\delta=10,\quad r=28,\quad b=8/3,
$$
y tomemos como valores iniciales los siguientes
$$
x(0)=1,\quad y(0)=0,\quad z(0)=0.
$$
Para resolverlo numéricamente usaremos el programa Maxima CAS (con licencia GNU) cuyo código está disponible desde aquí. Lo integraremos de \(t=0\) a \(t=100\) con un paso \(\Delta t=0.001\). Dicho programa usa un algoritmo muy preciso y estable para resolver ecuaciones diferenciales. Los resultados de la simulación se pueden ver en la gráfica izquierda en azul de la siguiente figura:
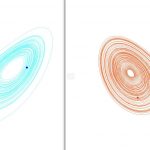
Cambiemos, como el propio Lorenz hizo, los valores iniciales una milésima. Por ejemplo, elijamos como valores iniciales los siguientes
$$
x(0)=1,\quad y(0)=0.001,\quad z(0)=0,
$$
donde hemos cambiado únicamente el valor de \(y(0)\). Los resultados se pueden ver en la gráfica derecha en rojo de la figura anterior.
A primera vista parecen muy parecidas, pero si nos fijamos, en ambas hay un punto negro en la parte de debajo. Dicho punto es el punto de partida de nuestro sistema \(\big(x(0),y(0),z(0)\big)\). También hay en ambas gráficas dos puntos que es el punto correspondiente a las coordenadas \(\big(x(100),y(100),z(100)\big)\). Como se ve claramente ambos ¡no coinciden!
Representemos ambas trayectorias juntas:
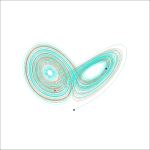
Como se ve, al principio ambas coinciden pero pasado un tiempo se separan. Esto se ve más claro si representamos los valores de la serie temporal de \(x(t)\), \(y(t)\) y \(z(t)\) por separado, lo cual mostremos en la siguiente figura:
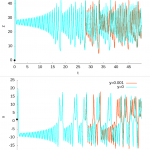

Como se ve en la figura anterior, en torno a \(t=27\) ambas funciones \(x(t)\) y \(z(t)\) empiezan a diferenciarse hasta no haber apenas ninguna similitud. Lorenz había descubierto, casi por azar, el primer ejemplo de lo que hoy denominamos la Ciencia del Caos.
Tras su descubrimiento el Lorenz matemático se puso también manos a la obra y encontró el mismo problema con sistemas parecidos al original (entre los que encontró el sistema (*) que aquí hemos usado). Y no solo, sus investigaciones le llevaron a descubrir cierto orden en el presunto caos (en su acepción de confusión, desorden) de la predicción del tiempo.
El trabajo pionero de Lorenz sobre el sistema (*) publicado en 1963 dio inicio a una serie de investigaciones sobre sistemas dinámicos que condujo a lo que hoy llamamos la Teoría del Caos, pero este caos no es el que se suele entender habitualmente, es decir: confusión, desorden; sino, como bien explica el diccionario de la RAE en su tercera acepción: Comportamiento aparentemente errático e impredecible de algunos sistemas dinámicos deterministas con gran sensibilidad a las condiciones iniciales.
Antes de concluir nuestra entrada tenemos que destacar que el propio Poincaré era consciente de que lo que descubrió Lorenz era una posibilidad muy real. De hecho la frase que transcribimos antes de su Ciencia y Método terminaba con estas proféticas palabras
Pero no siempre es así [poder predecir el fenómeno]; bien puede suceder que pequeñas diferencias en las condiciones iniciales produzcan unas [diferencias] muy grandes en los fenómenos finales. Un pequeño error en las primeras producirá un enorme error en los últimos. La predicción, entonces, se vuelve imposible, y nos encontramos con un fenómeno fortuito.
Como cuenta Gleick en una de las notas de su ya mencionado libro, la advertencia de Poincaré quedó prácticamente olvidada en los Estados Unidos (y no solo), a excepción quizá de George D. Birkhoff quien siguió el ejemplo de Poincaré en los años veinte y treinta y que casualmente fue durante un breve tiempo profesor de un joven Edward Lorenz en el MIT, aunque este reconoció que no era consciente del trabajo de Poincairé en Mecánica Celeste pues de haberlo sabido se hubiese centrado en un modelo más sencillo y no el de 12 variables con el que trabajaba en 1961. En efecto, como ya contamos en una entrada anterior, Poincaré descubrió al estudiar el famoso problema de los tres cuerpos que este era, de facto, un movimiento caótico en el sentido que la definición que da Steven H. Strogatz en su libro Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering
El caos es un comportamiento aperiódico a largo plazo en un sistema determinista que exhibe una dependencia sensible de las condiciones iniciales.
La explicación de las palabras en negrita (a excepción quizá de la dependencia sensible) de dicha definición requerirían de un largo apéndice matemático que el lector más matemático interesado puede descubrir en el citado libro de Strogatz, y el menos matemático en los textos de Gleick y Lorenz respectivamente. En cualquier caso, tras la lectura de esta entrada espero que el lector haya quedado convencido no solo de la que la propia física clásica esta infectada con la impredecibilidad (de lo que ya hablamos en la antes mencionada entrada), sino que la previsión del tiempo a largo plazo también lo está.
Para saber más:
[1] James Gleick, Caos: La creación de una ciencia. Editorial Crítica.
[2] Edward N. Lorenz, La esencia del caos, Debate
[3] Steven H. Strogatz, Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering. CRS (2024).
[4] Adilson E. Motter; David K. Campbell, Chaos at fifty, Physics Today 66 (5), 27–33 (2013).
Entradas relacionadas en el blog:
[5] Edward Lorenz (1917-2008): con él empezó el caos
[6] Determinismo o indeterminismo, esa es la cuestión
[7] Sobre la vida de Edward Lorenz se puede consultar, aparte de su libro [2], el artículo Edward Norton Lorenz y el efecto mariposa escrito por Francisco Maíz Jiménez (Suma: Revista para la enseñanza y el aprendizaje de las matemáticas, nº 79 (JUL-2015); pp. 97-108)

La imagen destacada es una superposición de una imagen de uno de los satélites de Meteosat superpuesta con la mariposa de Lorenz y las ecuaciones (*) que la producen.

Dejar una contestacion