Neither Euclid nor Archimedes

What is really more important: to propose a new method, or to make great use of it? To introduce a new concept that will be a keystone, or to develop it to the point of solving a famous problem? Different people will have different opinions, of course. Here is one opinion, that of Georg Cantor, on a related subject: “in mathematics, the art of proposing problems is more important than that of solving them”. (According to this, Cantor has more merit in proposing the Continuum Problem than Cohen in proving the independence of the Continuum Hypothesis from the Zermelo-Fraenkel axioms.)

Eudoxus of Cnidus, a mathematician of the 4th century B.C.E., is not the most famous of the ancient mathematicians, by any means. This, in my humble opinion, is unfair. I think that proposing problems and methods that have marked an entire epoch is more than enough reason to consider a mathematician a genius. This is what our protagonist did. Eudoxus led the way in working with incommensurable quantities, a very serious problem that had arisen in the 5th century, and introduced the famous method of exhaustion; he also established the framework within which all Greek and Hellenistic mathematical astronomy developed. No less!

It gets worse, because some of the literature circulating about Eudoxus is unreliable. Wikipedia says that “he was a philosopher, astronomer, mathematician and physician of Ancient Greece, a pupil of Plato”. The latter is not known to us: he visited Athens a couple of times, but it is not very clear that his relations with Plato were good; perhaps the Athenian was jealous of the great mathematician and astronomer. More important, it seems, were his trips to Egypt, to Heliopolis in particular, where he learned astronomy from the wise Egyptians. But Plato’s followers were always keen to present their master as the origin of the great achievements of ancient astronomy, so it was very convenient to portray Eudoxus as a mere pupil.

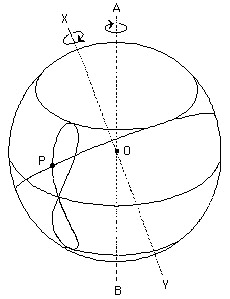According to reliable sources, Eudoxus initiated the path of classical Greek astronomy, with its basic principles: the motion of the planets, despite their erratic appearance (retrogradations), was “in fact” the result of simple circular and uniform motions. He proposed a geometrical model of homocentric spheres which, by combining two interlocking spheres, gave rise to movements in the shape of an 8, specifically the figure of the hippopede or spherical lemniscata. And with this, together with a translational movement, the apparent orbits (considered as geocentric) of planets such as Jupiter or Saturn were simulated quite well. An interesting animation can be seen in the video ‘Eudoxus explained’ on YouTube.

In geometry, we know of his decisive contribution to the classical theory of proportion, which would later be taken up by Euclid in the Elements, book V. (See also Aristotle, Second Analytics, 14a 17-25; Proclus, In I Euclidis Comm… 55.18-23, as Luis Vega points out in a wonderful biography in Divulgamat.) The great merit of this theory has often been pointed out, that it made it possible to work rigorously with incommensurable quantities, despite not being able to measure them with rational fractions. It has been said that Eudoxus was something like the Greek Dedekind, although there are some fundamental differences between the theory of real numbers (Dedekind’s and others’) and the Greek theory of incommensurables. In particular, the Greeks never established enough principles to deduce the completeness or ‘continuity’ of the domain of the real numbers (or of the corresponding domain of quantities).

We also have evidence that Eudoxus succeeded in proving two theorems glimpsed by Democritus: that the volume of a pyramid is one third of the volume of a prism with the same base and height; and that the volume of a cone is one third of the volume of a cylinder with the same base and height (see Archimedes, preface to On the Sphere and the Cylinder and preface to Method). The proofs of these theorems rested on the use of a method of “convergence” – as Vega puts it – which is often called the method of exhaustion. It rests on the theory of proportion and on certain implicit assumptions that Archimedes would later formulate (although Aristotle already writes that “by always adding something to the finite we will exceed every finite magnitude”, Physics, 266a 2-4).

With all this in mind, I would venture to state that, as a creative mathematician, Eudoxus was a greater figure than Euclid. And I conclude by asking the reader: who was greater, Archimedes or Eudoxus? It is well known, though, that some questions are not sufficiently well formulated to admit of a clear answer…

Reference

Eudoxus biography by Luis Vega