
26 April 2020 marks the 100th anniversary of the death of the brilliant Indian mathematician Srinivasa Ramanujan who, with minimal academic education, made extraordinary contributions to mathematical analysis, number theory, series and continued fractions. Ramanujan was born on 22 December 1887 and, after years of self-taught work in India, completely isolated from the mathematical community, he sent his famous letter to the British mathematician G. H. Hardy in January 1913, in which he shared with him a few of the results he had obtained. Hardy appreciated Ramanujan’s genius and managed to bring him to Cambridge, where they collaborated for almost five years. Ill – he was diagnosed with tuberculosis, possibly wrongly – he returned to India in 1919, and died shortly afterwards, aged 32.
In addition to 37 publications in research journals, 7 of them the result of his collaboration with Hardy, he left us his famous “notebooks”, with an astonishing collection of unconventional results, most of them without demonstration. Studying the contents of these notebooks and providing rigorous proofs of the formulae contained therein has been the subject of study by a large number of mathematicians throughout the 20th century.
It is not the aim of these notes to give an overview of Ramanujan’s life and work, but simply to show the best known result obtained by him and Hardy, and which is repeatedly referred to in the biographical film “The Man Who Knew Infinity”. This is the calculation of the number of partitions. We will begin by explaining the problem and analysing what was known before Ramanujan came on the scene, and in a future entry we will conclude with Hardy’s and Ramanujan’s advances, as well as Rademacher’s final improvement.
Number of partitions
Given \(n\) a positive integer, a partition of \(n\) is any sum of
\[ a_1 + a_2 + \cdots + a_r = n,\]
where the \(a_j\) are also positive integers (they need not be distinct from each other). Two partitions that differ only in the order of the addends are not considered distinct.
If \(k_j\) is the number of times \(a_j\) appears in the sum, then we can also put
\[ k_1 a_1 + k_2 a_2 + \cdots + k_s a_s = n.\]
Here, the \(a_j\) are already all distinct, and we can even think of the sum as involving all the integers \(a_j\), with all but a finite number of \(k_j = 0\).
We want to know the number of partitions of \(n\), that is, how many ways can we write \(n\) as a sum of positive integers? We will denote this number by \(p(n)\).
Calculating the number of partitions is not a simple combinatorial problem. Its origin goes back to Leibniz, who proposed it in a letter dated 1696, and it was Euler who first made some significant progress in its study.
For small \(n\), calculating \(p(n)\) by hand has no difficulty. For example,
\[ 5 = 4 + 1 = 3 + 2 = 3+1+1 = 2+2+1 = 2+1+1+1 = 1+1+1+1+1,\]
so \(p(5) = 7\).
But, as seen in the table below, the number of partitions grows considerably with \(n\), and no pattern is observed:
\[
\begin{array}{rr@{\qquad\,}rr@{\qquad\,}rr@{\qquad\,}rr@{\qquad\,}rr}
\hline
n\; & p(n)\!\!\!\! & n\; & p(n)\! & n\; & p(n)\, & n\; & p(n)\,\, & n\; & p(n)\,\,\, \\
\hline
1 & 1 & 13 & 101 & 25 & 1958 & 37 & 21637 & 49 & 173525 \\
2 & 2 & 14 & 135 & 26 & 2436 & 38 & 26015 & 50 & 204226 \\
3 & 3 & 15 & 176 & 27 & 3010 & 39 & 31185 & 51 & 239943 \\
4 & 5 & 16 & 231 & 28 & 3718 & 40 & 37338 & 52 & 281589 \\
5 & 7 & 17 & 297 & 29 & 4565 & 41 & 44583 & 53 & 329931 \\
6 & 11 & 18 & 385 & 30 & 5604 & 42 & 53174 & 54 & 386155 \\
7 & 15 & 19 & 490 & 31 & 6842 & 43 & 63261 & 55 & 451276 \\
8 & 22 & 20 & 627 & 32 & 8349 & 44 & 75175 & 56 & 526823 \\
9 & 30 & 21 & 792 & 33 & 10143 & 45 & 89134 & 57 & 614154 \\
10 & 42 & 22 & 1002 & 34 & 12310 & 46 & 105558 & 58 & 715220 \\
11 & 56 & 23 & 1255 & 35 & 14883 & 47 & 124754 & 59 & 831820 \\
12 & 77 & 24 & 1575 & 36 & 17977 & 48 & 147273 & 60 & 966467 \\
\hline
\end{array}
\]
There are two key questions to ask:
- Is there a “closed formula” that gives \(p(n)\) for any \(n\)?
- Can we estimate the size of \(p(n)\) when \(n\) is large?
Euler’s work
The partition generating function
The first important advance in the study of the number of partitions came from Euler, who managed to write the \(p(n)\) by means of a generating function.
Let us recall that, in general, we call the generating function of a sequence \(\{a(n)\}_{n=0}^{{infty}\) a function \(G(x)\) whose Taylor development is
\[ G(x) = \sum_{n=0}^{\infty} a(n) x^n.\]
What Euler proved for the number of partitions \(p(n)\) is that, if we also take \(p(0) = 1\), it verifies
\[ \prod_{m=1}^{\infty} \frac{1}{1-x^{m}} = \sum_{n=0}^{\infty} p(n) x^n \]
for \(|x| < 1\).
Actually, and if we skip the details of convergence, the formula is not difficult to prove. If we develop
\[ \prod_{m=1}^{\infty} \frac{1}{1-x^{m}} = (1+x+x^2+\cdots) (1+x^2+x^4+\cdots) (1+x^3+x^6+\cdots) \cdots \\ = 1 + \sum_{n=1}^{\infty} a(n) x^n, \]
we want to find that \(a(n) = p(n)\).
Suppose we have taken the term \(x^{n_1}\) from the first series, \(x^{2n_2}\) from the second, \(x^{3n_3}\) from the third,… and the term \(x^{kn_k}\) from the \(k\)-th (with \(n_i\ge0\)). Their product is \(x^{n_1} x^{2n_2} x^{3n_3} \cdots x^{kn_k} = x^n\), therefore
\begin{align*}
n &= n_1 + 2n_2 + 3n_3 + \cdots + kn_k \\
&= (\underbrace{1+1+\cdots+1}_{n_1}) + (\underbrace{2+2+\cdots+2}_{n_2}) + \cdots
+ (\underbrace{k+k+\cdots+k}_{n_k}),
\end{align*}
and this is a partition of \(n\) into positive summands.
Each partition of \(n\) will produce a \(x^n\) term and, reciprocally, each \(x^n\) term comes from a suitable partition of \(n\). Therefore, \(a(n)\) (the coefficient of \(x^n\)) is equal to \(p(n)\) (the number of partitions of \(n\)), as we were looking for.
Relation to pentagonal numbers
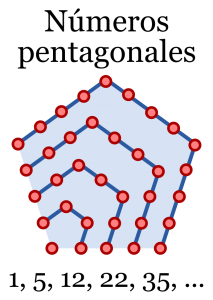
The next step in finding a formula for \(p(n)\) requires, surprisingly, talking about pentagonal numbers.
By definition, the \(n\)-th pentagonal number \(p_n\) is the number of points in the superposition of \(n\) regular pentagons in the pattern shown on the right.
As shown in the drawing, each new pentagon adds \(4\) vertices and \(3\) edges, so that
\[
p_n = p_{n-1} + 4 + 3(n-2).
\]
By induction (for example), we get
\[
p_n = \frac{n(3n-1)}{2}, \quad n=1,2,3,\dots.
\]
So, the first pentagonal numbers are
\[
1, 5, 12, 22, 35, 51, 70, 92,\dots
\]
If in the same formula of the pentagonal numbers we take indices \(k \in \mathbb{Z}\) we have the so-called generalised pentagonal numbers:
\[
g_k = \frac{k(3k-1)}{2}, \quad k = 0, 1, {-1}, 2, {-2}, 3, {-3},\dots
\]
The first ones are
\[
0, 1, 2, 3, 5, 7, 12, 15, 22, 26, 35, 40, 51, 57, 70, 77, 92,\dots
\]
In 1750, Euler proved that, when multiplying
\[
(1-x)(1-x^{2})(1-x^{3}) \cdots
= 1-x-x^{2}+x^{5}+x^{7}-x^{12}-x^{15}+x^{22}+\cdots
\]
many exponents cancel, and the remaining ones are precisely the generalised pentagonal numbers. In particular, what is obtained is the so-called Euler pentagonal number theorem:
\[
\prod_{n=1}^{\infty} \left(1-x^{n}\right)
= \sum_{k=-\infty}^{\infty}(-1)^{k} x^{k(3 k-1)/2}.
\]
This theorem is of great importance in the calculation of \(p(n)\),
and there are several ways of proving it. In addition to Euler’s original proof (by induction), there are proofs by Legendre (1830), Jacobi (1846) and Franklin (1881, with combinatorial arguments).
Euler’s recursive formula
Using the pentagonal number theorem combined with the generating function of the partitions, we have
\[
1 = \prod_{n=1}^{\infty} \left(1-x^{n}\right)
\prod_{m=1}^{\infty} \frac{1}{1-x^{m}}
= \Big(1 + \sum_{k=1}^{\infty}(-1)^{k} (x^{g_k} + x^{g_{-k}}) \Big)
\cdot \sum_{n=0}^{\infty} p(n) x^n.
\]
Multiplying both expressions leads us to the fact that, if we take \(p(0) = 1\) and \(p(n) = 0\) if \(n<0\), for \(n \ge 1\) we can write
\[
p(n) – p(n-1) – p(n-2) + p(n-5) + p(n-7) + \cdots = 0,
\]
or else,
\[
p(n) = \sum_{k=1}^{\infty} (-1)^{k+1} \big(p(n-g_k)+p(n-g_{-k})\big)
\]
(from a certain \(k\), the summands are all null, so this series is actually a finite sum).
This recursive formula, due to Euler, allows us to calculate \(p(n)\) with relative ease, and is the best there was until Ramanujan became interested in the subject; that will be considered in a future post.
Many of the details of Euler’s work can be found in [2]; in particular, in the superb facsimile edition (translated and annotated) [3]. If the reader is interested in a more up-to-date treatment, it can be found in [1].
Referencias
[1] T. M. Apostol, Introducción a la Teoría Analítica de Números, Reverté, Barcelona, 1980.
[2] L. Euler, Introductio in analysin infinitorum (1748), cap. 16, «De partitione numerorum», Opera omnia, ser.1, 8; «De partition enumerorum» (1753), Opera omnia, ser. 1, 2, p. 280.
[3] L. Euler, Introductio in analysin infinitorum, (Introduction to the analysis of the infinite), edited by A. J. Durán y F. J. Pérez, 2 vols. (facsimile and critical edition), SAEM Thales and Real Sociedad Matemática Española, Sevilla, 2000.

Leave a Reply