Ni Euclides ni Arquímedes

¿Qué es más importante: proponer un nuevo método, o sacar gran partido de él? ¿Introducir un concepto nuevo que será clave, o desarrollarlo hasta resolver un problema famoso? Distintas personas opinarán de distinta manera, claro. Aquí va una opinión, la de Georg Cantor, sobre un tema relacionado: “en cuestiones matemáticas, el arte de proponer problemas es más importante que el de resolverlos”. (Según esto, tiene más mérito Cantor al proponer el Problema del Continuo, que Cohen al demostrar la independencia de la Hipótesis del Continuo de los axiomas de Zermelo-Fraenkel.)

Eudoxo de Cnido, matemático del siglo IV a.n.e., no es el más famoso de los matemáticos antiguos, ni mucho menos. Esto, en mi modesta opinión, es injusto. Pienso que proponer problemas y métodos que han marcado toda una época, es motivo más que suficiente para considerar a un matemático genial. Esto es lo que hizo nuestro personaje. Eudoxo marcó el camino para trabajar con las cantidades inconmensurables, problema muy serio que había surgido en el siglo V, e introdujo el célebre método de exhausción; además estableció el marco o el patrón dentro del que se desarrolló toda la astronomía matemática griega y helenística. ¡Nada menos!

La cosa es peor aún, porque parte de la información que circula sobre Eudoxo es poco fiable. Wikipedia dice que “fue un filósofo, astrónomo, matemático y médico de la Antigua Grecia, pupilo de Platón”. Esto último no nos consta: visitó un par de veces Atenas, pero no está muy claro que sus relaciones con Platón fueran buenas; quizá el ateniense sintió celos del gran matemático y astrónomo. Parece que fueron más importantes sus viajes a Egipto, a Heliópolis concretamente, donde aprendió astronomía de los sabios egipcios. Pero los seguidores de Platón tenían mucho interés en presentar a su maestro como el origen de los grandes logros de la astronomía antigua, así que era muy conveniente pintar a Eudoxo como un simple pupilo.

Según fuentes fiables, Eudoxo inició la vía de la 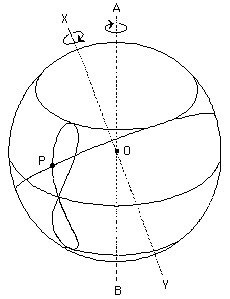astronomía griega clásica, con sus principios básicos: el movimiento de los planetas, pese a su apariencia errática (retrogradaciones), era “en realidad” el resultado de movimientos simples circulares y uniformes. Propuso un modelo geométrico de esferas homocéntricas que conseguía, combinando dos esferas engranadas, dar lugar a movimientos en forma de 8, concretamente a la figura de la hipopeda o lemniscata esférica. Y con ello, unido a un movimiento de traslación, se simulaban bastante bien las órbitas aparentes (consideradas como geocéntricas) de planetas como Júpiter o Saturno. Puede verse una interesante animación en el video ‘Eudoxus explained’ en YouTube.

En geometría, conocemos su contribución decisiva a la teoría clásica de la proporción, que luego sería recogida por Euclides en los Elementos, libro V. (Se puede ver también Aristóteles, Segundos Analíticos, 14a 17-25; Proclo, In I Euclidis Comm., 55.18-23, tal como señala Luis Vega en una estupenda biografía de Eudoxo recogida en Divulgamat.) Se ha señalado muchas veces el gran mérito de esta teoría, que permitía trabajar rigurosamente con cantidades inconmensurables, a pesar de no poder medirlas con fracciones racionales. Se ha dicho que Eudoxo fue algo así como el Dedekind griego, si bien hay algunas diferencias fundamentales entre la teoría de los números reales (de Dedekind y otros) y la teoría griega de inconmensurables. En concreto, los griegos nunca establecieron principios suficientes para deducir la completitud o ‘continuidad’ del dominio de los reales (o del dominio equivalente de las cantidades).

Nos consta también que Eudoxo consiguió demostrar dos teoremas entrevistos por Demócrito: que el volumen de una pirámide es un tercio del volumen de un prisma con igual base y altura; y que el volumen de un cono es un tercio del volumen de un cilindro con su misma base y altura (véase Arquímedes, prefacio de Sobre la esfera y el cilindro y prefacio del Método). Las pruebas de estos teoremas descansaban en el uso de un método de “convergencia” —como dice Vega— que suele llamarse método de exhausción. Descansa en la teoría de la proporción y en ciertos supuestos implícitos que formularía luego Arquímedes. (Aunque ya Aristóteles escribe que «al agregarle siempre algo a lo finito excederemos toda magnitud finita», Física, 266a 2-4.)

Teniendo todo esto en cuenta, me atrevo a firmar que, como matemático creativo, Eudoxo fue una figura mayor que Euclides. Y termino preguntando al lector: ¿quién fue más grande, Arquímedes o Eudoxo? Aunque ya se sabe que algunas preguntas no están lo bastante bien formuladas como para admitir respuesta clara…

Referencia:

Biografía de Luis Vega en https://www.divulgamat.net