
¿Eh? ¿Qué es eso de conmemorar que algo cumple 46 años? ¿Se ha vuelto loco este autor? (incluso si me conoces, no te sientas obligado a remitirme tu opinión). Es cierto que todos estamos acostumbrados a celebrar de manera especial los centenarios, o incluso los aniversarios 10, 25, 50 o 75, pero los matemáticos sabemos que eso es una mera cuestión cultural, fruto de que contamos en base 10. De hecho, el número 46 puede ser tan bonito como cualquier otro, y tiene interesantes propiedades que lo hacen único; por ejemplo, es el mayor número par que no se puede expresar como suma de dos números abundantes. Así pues, no tiene nada de raro que, en este año 2020 recién estrenado, recordemos la conjetura que, en 1974, nos dejaron Hsiang-Tsung Kung y su director de tesis Joseph Frederick Traub en su artículo [2]. La conjetura de Kung-Traub es, realmente, muy poco conocida fuera del ámbito de los analistas numéricos dedicados a los métodos iterativos para resolver ecuaciones no lineales (de hecho, y en el momento de escribir estas líneas, ¡ni siquiera tiene su propia entrada en la Wikipedia!) así que, antes de explicarla, debo entrar un poco en la materia.

Supongamos que tenemos una función \(f\) de \(\mathbb{R}\) en \(\mathbb{R}\) (de hecho, no hace falta que el dominio sea todo \(\mathbb{R}\)), y que dicha función es suficientemente buena, es decir, que es continua y va a tener tantas derivadas como convenga en las argumentaciones que siguen. Así mismo, sea \(x^{*}\) una raíz de \(f\), que consideramos simple.

Si el valor de la raíz no lo conocemos, hay muchas maneras de encontrarlo de manera aproximada. Por ejemplo, podemos buscar dos puntos \(a\) y \(b\) en los que \(f(a)\) y \(f(b)\) tengan distinto signo y utilizar el método de la bisección, o el de la secante, con lo cual, reiterando, forzosamente nos acercaremos cada vez más a una raíz \(x^{*}\) entre \(a\) y \(b\).
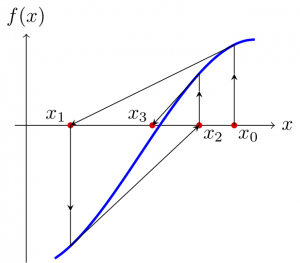
Otra alternativa es utilizar el método de la tangente, también denominado de Newton o de Newton-Raphson. Elegimos un punto \(x_0\) cercano a la raíz \(x^{*}\) que buscamos e iteramos mediante
$$
x_{n+1} = x_n – \frac{f(x_n)}{f'(x_n)}, \quad n=0,1,2,\dots.
$$
Bajo determinadas circunstancias que no detallaremos, la sucesión \(\{x_n\}_{n=0}^{\infty}\) convergerá a la raíz. Aunque la interpretación geométrica se pierde, el método iterativo que acabamos de describir también puede usarse para encontrar raíces de funciones de \(\mathbb{C}\) en \(\mathbb{C}\), y lo mismo ocurrirá en adelante. (De hecho, también se puede adaptar para buscar raíces de funciones definidas en \(\mathbb{R}^d\), \(\mathbb{C}^d\), o incluso a espacios de Banach, pero eso está fuera de lo que aquí queremos exponer.)
Hay muchos otros métodos iterativos destinados a encontrar raíces. Por ejemplo, el método de Halley
$$
x_{n+1} = x_{n} – \frac{2 f(x_{n}) f'(x_{n})}{2(f'(x_{n}))^{2}-f(x_{n})f^{\prime\prime}(x_{n})}
$$
o el de Chebychev
$$
x_{n+1} = x_{n} –
\frac{f(x_{n})}{f'(x_{n})} \left(1+\frac{f(x_{n})f^{\prime\prime}(x_{n})}{2(f'(x_{n}))^{2}}\right).
$$
En el libro [6] o en los artículos [3] o [7] se pueden ver bastantes más.
Cuando dichos métodos se aplican a funciones complejas, la dinámica de los métodos iterativos para resolver ecuaciones pueden dar lugar a preciosos dibujos (además de [1] o el ya citado [7], también conviene mencionar [5], que efectúa un estudio más teórico), pero no es esto lo que nos ocupa ahora.
Dado que hay distintos métodos con el mismo objetivo de encontrar raíces de funciones, nos puede convenir usar uno u otro dependiendo de diversas circunstancias. Por ejemplo, la exigencia sobre el punto inicial \(x_0\) para que se garantice la convergencia del método a una raíz, el número de iteraciones requerido para que la aproximación sea buena, la velocidad de ejecución de cada paso del método, la estabilidad, etc. Un criterio importante es el orden de convergencia. Se dice que un método iterativo \(x_{n+1} = I_f(x_{n})\) destinado a encontrar una raíz simple \(x^{*}\) de \(f\) tiene orden \(p>1\) si, tras comenzar en un punto \(x_0\) suficientemente cerca de \(x^{*}\), se cumple
$$
\lim_{n \to \infty} \frac{|x^{*}-x_{n+1}|}{|x^{*}-x_{n}|^{p}} = C \neq 0.
$$
Por ejemplo, el método de Newton tiene orden \(2\), y los Halley y Chebychev tienen orden \(3\). En principio, cuanto más alto sea el orden, menos iteraciones se necesitarán para aproximar \(x^{*}\) con la precisión que deseemos.
Pero, claro, hay que tener en cuenta el trabajo que cuesta efectuar cada paso del método, y ahí es fundamental considerar el número de evaluaciones de la función o de sus derivadas (estamos suponiendo que, en principio, cuesta el mismo trabajo evaluar \(f\) que cualquiera de sus derivadas involucradas en el método iterativo). El método de Newton requiere dos evaluaciones, pero los métodos de Halley y Chebychev requieren tres, así que, en este sentido, no podemos decir que los de Halley y Chebychev sean mejores métodos que el de Newton, pese a tener orden de convergencia mayor.
Es fácil convencerse de que, si tenemos un método iterativo de orden \(p\) y otro de orden \(q\), y en cada paso los aplicamos sucesivamente, encontramos un método de orden \(pq\). Por ejemplo, si en cada paso aplicamos dos veces el método de Newton, tenemos el siguiente método de orden \(4\):
$$
\begin{cases}
y_{n} = x_{n} – \frac{f(x_{n})}{f'(x_{n})}, \\[4pt]
x_{n+1} = y_{n} – \frac{f(y_{n})}{f'(y_{n})}.
\end{cases}
$$
Pero en el método de Newton evaluábamos una vez \(f\) y otra \(f’\), y ahora estamos evaluando dos veces \(f\) y otras dos \(f’\), con lo cual no estamos ganando nada (lo contrario sería milagroso). La buena noticia es que el orden \(4\) se puede mantener sustituyendo una de estas evaluaciones por alguna combinación de las demás. Así, por ejemplo, tenemos el método de Ostrowski
$$
\begin{cases}
y_{n} = x_{n} – \frac{f(x_{n})}{f'(x_{n})}, \\[4pt]
x_{n+1} = y_{n} – \frac{f(y_{n})(y_{n}-x_{n})}{2 f(y_{n})-f(x_{n})}
\end{cases}
$$
que tiene orden \(4\) y que, en cada paso, solo evalúa dos veces \(f\) y una vez \(f’\). En este sentido, el método de Ostrowski es mejor que los métodos de Halley y de Chebychev pues, con el mismo número de evaluaciones, tiene orden de convergencia mayor.
Si combinamos el método de Ostrowski con el de Newton tendríamos
$$
\begin{cases}
y_{n} = x_{n} – \frac{f(x_{n})}{f'(x_{n})}, \\[4pt]
z_{n} = y_{n} – \frac{f(y_{n})(y_{n}-x_{n})}{2 f(y_{n})-f(x_{n})}, \\[4pt]
x_{n+1} = z_{n} – \frac{f(z_{n})}{f'(z_{n})},
\end{cases}
$$
un método de orden \(8\) pero con cinco evaluaciones de \(f\) o \(f’\). De nuevo se puede evitar una de las evaluaciones, consiguiendo un método de orden \(8\) que solo requiere cuatro evaluaciones. No importa aquí cómo se hace; de hecho, hay muchísimos métodos iterativos de orden \(8\) con cuatro evaluaciones, como puede verse en [1], que compara 29 de tales métodos.
¿Hasta dónde se puede conseguir esto? ¿Siempre se va a poder eliminar una evaluación manteniendo el orden? ¿Hasta qué orden se puede llegar con \(d\) evaluaciones? Realmente, no se sabe, y el lector habrá podido adivinar que la conjetura de Kung-Traub tiene una opinión al respecto.
Para dejar las cosas claras, ya sólo necesitamos dar un par de definiciones. Un método iterativo se denomina sin memoria cuando para calcular \(x_{n+1}\) sólo hace falta conocer \(x_n\), pero no \(x_{n-1}\) ni los anteriores; en este sentido, los métodos de la bisección o de la secante requieren memoria (para efectuar un nuevo paso, necesitamos los dos puntos anteriores), pero el de Newton o el resto de los métodos iterativos que hemos visto aquí son métodos sin memoria. Por otra parte, un método se denomina unipunto si, en cada paso, la función y/o sus derivadas se evalúan en un único punto, y multipunto si se evalúan en varios puntos; por ejemplo, los métodos de Newton, Halley y Chebychev son unipunto (en cada paso, sólo se evalúa \(f\) y las derivadas en \(x_{n}\)), pero el de Ostrowski es multipunto (se efectúan evaluaciones en \(x_{n}\) y en \(y_{n}\)).
En [6, teorema 5-3], Traub había probado que un método unipunto para resolver una ecuación no lineal de la forma \(f(x) = 0\), que efectúe una evaluación de la función dada \(f\) y de cada una de sus \(p-1\) primeras derivadas, puede alcanzar, como máximo, orden de convergencia \(p\). Esto despertó el interés por el estudio de los métodos multipunto, que no estaban constreñidos por ese límite teórico para el orden de convergencia, y por tanto podían permitir mayor eficiencia computacional.
En 1974, Kung y Traub [2] enunciaron lo que ahora se conoce como conjetura de Kung-Traub: un método iterativo multipunto (y sin memoria) para encontrar raíces simples de una función puede alcanzar, como máximo, orden de convergencia \(2^{d-1}\), donde \(d\) es el número total de evaluaciones de la función o sus derivadas.
Los métodos multipunto que satisfacen la conjetura de Kung-Traub se denominan habitualmente métodos óptimos. Para orden \(2\), \(4\), \(8\) y \(16\), los métodos óptimos efectúan, respectivamente, \(2\), \(3\), \(4\) y \(5\) evaluaciones. Está demostrado teóricamente que existen métodos óptimos para cualquier número de evaluaciones \(d\) (ver, por ejemplo, [2], [3, sección 3] o [4, sección 5]), pero no está descartado que el orden \(2^{d-1}\) se pueda superar.
Para finalizar, y para no incurrir en equívocos, creo importante hacer unas pocas consideraciones sobre estos métodos iterativos de orden muy alto. A grandes rangos, que el orden del método sea \(p\) significa que el número de dígitos correctos entre la raíz \(x^{*}\) y su aproximación \(x_n\) se multiplica por \(p\) en cada iteración. Así pues, los métodos de orden alto proporcionan, con muy pocas iteraciones, una extraordinaria precisión para la raíz buscada, con cientos o miles de dígitos correctos; eso sí, siempre que partamos de un punto «cercano» a la raíz. La búsqueda de métodos óptimos tiene su indudable interés teórico, pero, en la práctica, rara vez se requieren métodos de orden muy alto. A menudo es más razonable dedicar el esfuerzo a intentar localizar buenos puntos de partida para el método iterativo; o, desde un punto de vista teórico, a probar condiciones que garanticen la convergencia de un método desde zonas de partida suficientemente amplias. Si un método tiene un orden de convergencia muy alto, pero es difícil encontrar un punto inicial que converja a la raíz buscada, en la práctica no va a tener mucha utilidad. Pero no era de esto de lo que aquí estábamos hablando.
Referencias
[1] C. Chun y B. Neta, Comparative study of eighth-order methods for finding simple roots of nonlinear equations, Numer. Algorithms 74 (2017), no. 4, 1169-1201.
[2] H. T. Kung y J. F. Traub, Optimal order of one-point and multipoint iteration, J. Assoc. Comput. Mach. 21 (1974), no. 4, 643-651.
[3] M. S. Petković, On a general class of multipoint root-finding methods of high computational efficiency, SIAM J. Numer. Anal. 47 (2010), no. 6, 4402-4414; Remarks on “On a general class of multipoint root-finding methods of high computational efficiency”, SIAM J. Numer. Anal. 49 (2011), no. 3, 1317-1319.
[4] M. S. Petković y L. D. Petković, Families of optimal multipoint methods for solving nonlinear equations: a survey, Appl. Anal. Discrete Math. 4 (2010), no. 1, 1-22.
[5] S. Plaza y J. M. Gutiérrez, Dinámica del método de Newton, Universidad de La Rioja, Logroño, 2013.
[6] J. F. Traub, Iterative Methods for the Solution of Equations, Prentice Hall, Englewood Cliffs, N.J., 1964.
[7] J. L. Varona, Graphic and numerical comparison between iterative methods, Math. Intelligencer 24 (2002), no. 1, 37-46.

Es la primera vez que voy a opinar sobre un artículo de un blog al que he llegado casualmente. Estaba haciendo una búsqueda sobre métodos numéricos óptimos y afortunadamente el motor de Google me ha mostrado esta página entre las primeras opciones. Me ha encantado la exposición del tema para llegar a enunciar la conjetura de Kung-Traub que me parece muy estimulante por lo fácil que es de entender y lo difícil que está siendo de probar. No soy experto en Análisis Numérico aunque mi investigación actual me está empujando a aprender a marchas forzadas sobre el tema, además, no sólo estoy aprendiendo del tema sino que estoy conociendo a gente muy interesante como el autor de este artículo, el profesor Juan Luis Varona, al que felicito por la clara y motivadora exposición. Esto me ha llevado a buscar información sobre el profesor Varona y he visto su impresionante trayectoria, es una alegría tener a científicos tan interesantes cerca de nosotros y es una lástima no conocerlos, la diversidad de la investigación provoca que sólo conozcamos a aquellos que hacen cosas relativamente cercanas. Gracias por el trabajo.
No sé si es habitual firmar los comentarios pero no creo que deba ser algo anónimo, mi nombre es F. Javier Toledo Melero y soy profesor titular de universidad en la Universidad Miguel Hernández de Elche.