One of the most famous anecdotes about mathematics tells us that Hippasus of Metapontion (a Greek colony in the gulf of Tarentum, at the end of the peninsula that is now Italy) was thrown into the sea by his sect: the Pythagoreans. The cause, nothing more and nothing less than the discovery of irrational numbers.
It is actually rather obscure what was done by whom, and why Hippasus (or whoever) was punished: was it for finding irrationalities, or because of the dodecahedron? Was it for discovering a result, or for breaking the rule of silence of the Pythagoreans? On this, see the text of Iamblichus in the note I add at the end.
In any case, many historians are willing to defend that Hippasus of Metapontion may well have been the one who, around 450 BC, first discovered a geometrical relation that was not expressible as a fraction. An enormous discovery that marked the history of Pythagoreanism (the only metaphysical doctrine that has been refuted by demonstration) and the history of mathematics in Greece.
I would like to say something about how Hippasus, or some other Pythagorean back in the 5th century BC, some 2500 years ago, was able to make his great discovery.
The reader is probably familiar with the famous demonstration (by reductio ad absurdum) of the irrationality of the diagonal of the square. One begins by assuming that \(\surd(2)\) = a/b, where a and b are natural numbers; but in developing consequences of this assumption one arrives at a contradiction (which can be formulated by saying: b must be even, but also odd). But today I don’t want to talk about that proof: it is more likely that Hippasus’ discovery was about the diagonal of the pentagon.
The study of the pentagon connects with the dodecahedron, the “sphere of twelve pentagons” mentioned by the neo-Platonic Iamblichus (see note); the dodecahedron, indeed, fascinated the Pythagoreans. Pentagons are studied in Book IV of Euclid’s Elements, and there is reason to think that the content of that book comes from the Pythagoreans.
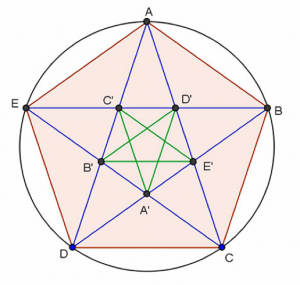As is well known, the mystical pentagram played a central role for them. (This pentagram is formed by the five blue lines in the figure, each of which is a diagonal of the pentagon.) And it is not only probable that Hippasus worked on the pentagon, but extremely beautiful.
Moreover, we shall see that the result can be obtained, not by reductio ad absurdum (a very sophisticated procedure, not very plausible in the early stages of the development of geometry), but by something reminiscent of infinite descent. In my opinion, this makes it more plausible that the proposed path was that of a first discovery.
Indeed, the ratio of the side (in red) to the diagonal (in blue) of the pentagon is the famous number φ [phi], the golden ratio, which is irrational. How could this, the irrationality of φ, have been discovered by a Pythagorean around 450 BC, in the 5th century BC?
As my daughter would say, because they were divine. Let’s have a look.
The pentagon and the pentagram are truly admirable for the richness and harmony of the relationships that arise in them. The figure of the pentagram generates a new inverted pentagon, and so on ad infinitum, to infinity. This is a marvellous thing, the infinite repetition of the same relations.
But the reader should study the attached figure a little, familiarise her or himself with its forms: (s)he will immediately notice that isosceles triangles appear everywhere.
The most important is the triangle ADC formed by the diagonals and the side of the pentagon; it is called the golden triangle. This triangle is the one Euclid uses to construct a pentagon inscribed in a given circle (Book IV, prop. 11).
But there are other smaller isosceles triangles: AE’B and BD’E’, for example, are similar to ADC.
Analyse, dear reader, the figure, familiarise yourself with the many triangles that appear, and try to discover (knowing that the angles at the base of an isosceles are equal) what relationship there is between the angles of the golden triangle. You will be able to show, as the Pythagoreans did, that the angles at its base are exactly double the angle at the apex. Remarkable. (In modern notation, the angle at A is 36º, the angles at D and C are 72º.)
Let us now try, as Hippasus surely did, to discover something about the relations between the side and the diagonal, also taking into account the side of the interior pentagon A’B’C’D’E’ (and, why not, the diagonal B’E’ as well).
In order not to get lost, let’s call l1 and l2 the major and the minor side, respectively, d1 and d2 the corresponding diagonals.
Using the properties of isosceles triangles in the figure, we see that AE’ = l1. But we can also see, considering the triangle B’E’C (isosceles again), that E’C = d2. We will then conclude that d1 = l1 + d2, or if you like
d2 = d1 – l1.
We are moving towards a result.
What about the small side l2? Well, it is easy to see (by symmetry) that AD’ = E’C, and that leads us to l2 + d2 = l1. So that
l2 = l1 – d2.
Great. We are almost there.
Let us now try to think about what properties a supposed common measure of the diagonal and the side, d1 and l1, would have. It would be, if it exists, a small fraction of the side l1 that “measures” the diagonal d1 –that is, exactly and without remainder–.
Let’s call m the common measure, that small portion of l1. Well, since d2 is the difference between d1 and l1 (both exact multiples of m), there is no doubt that d2 will be an exact multiple of m as well.
But l2 is the difference between l1 and d2, and for the same reason the side l2 will be an exact multiple of m. Which throws us headlong into the abyss of the infinitely many similar copies of the pentagon that arise within it.
What holds for l1 and d1 will also hold for l2 and d2: they are all measured by m exactly.
Similarly, the small measure m must be the common measure of the subsequent side and diagonal, l3 and d3, and so on — l4 and d4, etc.– in a process of infinite descent.
Now the measure m, however small, would have to be a finite fraction of the side l1. But the argument shows us that it must be a common measure of a whole series of smaller and smaller segments, without in fact any lower limit to their size.
Which is downright impossible!
Hippasus, after much thought and racking his brains, was forced to conclude that the relationship between the side and the diagonal of the pentagon cannot be expressed as a fraction. The side is incommensurable with the diagonal! There is no common measure! Or to put it another way: φ is irrational.
He must have been shocked: not all relations in the cosmos are numerical relations! Pythagoras was wrong in his metaphysics! (Here, to say ‘numerical relation’ is the same as saying ‘fraction’: for the Greeks, numbers are always the natural numbers. That is why, strictly speaking, they did not discover ‘irrational numbers’, since this concept made no sense to them: they discovered that there are incommensurable segments, geometrical quantities that are not expressible in a ‘rational’ way, as fractions.)
And if he was overcome with horror, his fellow sect members may well have been overcome with fury: legend has it that they were travelling by boat in the Mediterranean when Hippasus made them aware of the result, and that they could not avoid the temptation to kill the messenger of such disastrous news. It may not be true, but the story is good: se non è vero, è ben trovato.
They threw him out to sea. They dealt well with the messenger, but that was not enough to put an end to the dark message. Such are the things of mathematical reason – of the logos, which is imposed on us in spite of ourselves, whether we like it or not.
Sketch by Dalí for his work “Leda atómica”, where we can see that the composition is built on the mystical pentagram.
NOTE: Iamblichus says in Vita Pythagorica, 34: “Of Hippasus it is said that he was a Pythagorean, and that, because he was the first to describe and make public the sphere of the twelve pentagons, he perished in the sea for his impiety, and yet received credit for the discovery, although it really belonged to HIM (for thus they refer to Pythagoras, and not by his name)”.
However, Iamblichus is not too reliable: a neo-Pythagorean and a Neoplatonist, echoing surely legendary narratives, he lived around the year 300, some three quarters of a millennium after the fact! And, by the way, many historians are wary of the quasi-religious obsession with attributing everything to Pythagoras.
Leave a Reply