This year 2017 marks the 100th anniversary of the birth of Edward N. Lorenz, American mathematician and meteorologist, a key figure in the birth of chaos theory.

Lorenz studied mathematics at Dartmouth College in New Hampshire and Harvard University in Cambridge, and from 1942 to 1946 he was in the US Air Force, working as a meteorologist. At the end of World War II, he studied meteorology and received his PhD from the Massachusetts Institute of Technology, where he taught until his retirement.
In 1963 he published his legendary paper “Deterministic Nonperiodic Flow” in the Journal of the Atmospheric Sciences, in which he showed how small perturbations in the initial data of a system could produce, over time, enormous effects.
Lorenz wondered why, if the equations and initial conditions were known, it was not possible to predict the weather three days from now with acceptable reliability. To try to understand what was going on, he simplified the equations of the Earth’s atmospheric circulation as much as possible (see [1]), and came up with the following three-dimensional deterministic nonlinear dynamical system, which now bears his name:
\(\left\{ \begin{array}{l} \displaystyle\frac{dx}{dt} = \sigma (y-x), \\ \displaystyle\frac{dy}{dt} = (\rho-z)x – y,\\ \displaystyle\frac{dz}{dt} = xy – \beta z, \end{array} \right.\)
where \(\sigma\), \(\beta\) and \(\rho\) are three positive parameters to which he assigned the values \(\sigma=10\), \(\beta=8/3\) and \(\rho=28\). Simplified to this point, the system is no longer useful for weather forecasting; however, it has the necessary ingredients to be representative of atmospheric motions and is the most famous and most studied deterministic chaos-theoretic model.
Despite its relatively simple appearance, the above system has no analytical solution, so Lorenz set about solving it with numerical methods and the help of a computer. Almost by chance, when he repeated some calculations by introducing values previously obtained but with a very slight rounding (taking only three decimal places to write less), he observed, to his great surprise, drastic changes in the results (the details of the story can be found in [2]). Thus, he was able to conclude the following:
- The evolution of each of the components \(x(t)\), \(y(t)\) and \(z(t)\) of the solution has an apparently random behaviour.
- If, in the space \(xyz\), we draw the succession of values that the solutions take in the course of time, we obtain a trajectory that rolls up on a curious two-lobed object (it is clearly seen in the following graph). It was the first example of what is now called a “strange attractor”.
- The introduction of a very small error in the initial data grows exponentially with the calculation, so that after a relatively small time, a radically different result is obtained. This highlights the sensitivity of the system to the initial conditions.
In the figure, with the same parameters \(\sigma\), \(\beta\) and \(\rho\) used by Lorenz, and starting from the initial conditions \(x(0)=y(0)=z(0)=1\), we show the trajectory in space described by the curve \((x(t), y(t), z(t))\) when \(t\) varies between \(1\) and \(30\) (we dispense with what happens with \(t\) between \(0\) and \(1\) to wait for the trajectory to “enter” the attractor and make it look better).
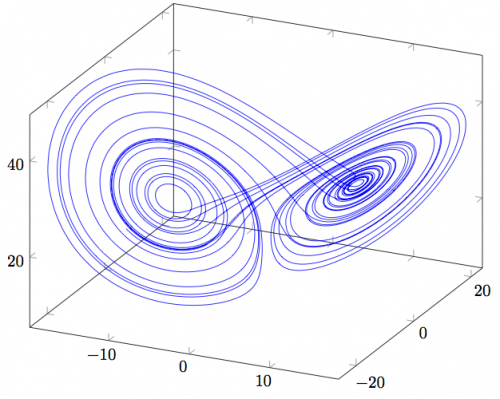
\((x(t), \, y(t), \, z(t))\) curve, solution of Lorenz’s equation.
If the highly simplified Lorenz model gives such chaotic behaviour, the behaviour of the real equations governing atmospheric weather – much more complicated, of course – cannot be expected to be any more predictable. If someone tells you what the weather will be like in your town in a month’s time, don’t believe it. Of course, if it is summer, it will tend to be hot; and, if it is winter, it will probably be cold.
Years later, Lorenz also introduced the concept of the “butterfly effect”, popularised in many ways, for example with the phrase “the flapping of a butterfly in Brazil can cause a tornado in Texas”. He wanted to explain the chaotic behaviour of unstable systems, such as weather, in which a small change in initial conditions – and, in practice, such conditions are impossible to know with complete accuracy – is magnified enormously as time progresses. That the Lorentz attractor resembles the wings of a butterfly is purely coincidental.
References
[1] M. Lezaun, Predicciones del Tiempo y Matemáticas, Bol. Soc. Esp. Mat. Apl. 22 (2002), 59-98.
[2] E. Lorenz, The Essence of Chaos, University of Washington Press, 1996.

Leave a Reply