The Kung-Traub conjecture turns 46 years old

Huh? What’s this about commemorating something being 46 years old? Has this author gone mad? (even if you know me, don’t feel obliged to send me your opinion). It is true that we are all used to celebrate centenaries, or even 10th, 25th, 50th or 75th anniversaries in a special way, but we mathematicians know that this is just a cultural thing, because we count in base 10. In fact, the number 46 can be as beautiful as any other, and it has interesting properties that make it unique; for example, it is the largest even number that cannot be expressed as the sum of two abundant numbers. So it is not surprising that, in this new year 2020, we remember the conjecture that, in 1974, Hsiang-Tsung Kung and his thesis supervisor Joseph Frederick Traub left us in their article [2]. The Kung-Traub conjecture is actually very little known outside the realm of numerical analysts dedicated to iterative methods for solving nonlinear equations (in fact, at the time of writing, it does not even have its own entry in Wikipedia!) so, before explaining it, I must go into the subject a little.

Let us suppose that we have a function \(f\) of \(\mathbb{R}\) on \(\mathbb{R}\) (in fact, the domain need not be all \(\mathbb{R}\)), and that this function is sufficiently good, that is, it is continuous and will have as many derivatives as is convenient in the following arguments. Likewise, let \(x^{*}\) be a root of \(f\), which we consider simple.

If we do not know the value of the root, there are many ways to find it approximately. For example, we can look for two points \(a\) and \(b\) in which \(f(a)\) and \(f(b)\) have different signs and use the bisection method, or the secant method, with which, iterating, we will necessarily get closer and closer to a root \(x^{*}\) between \(a\) and \(b\).

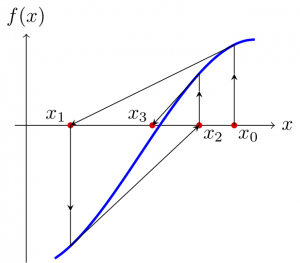
Another option is to use the tangent method, also known as Newton’s or Newton-Raphson’s method. We choose a point \(x_0\) close to the root \(x^{*}\) we are looking for and iterate by means of
$$
x_{n+1} = x_n – \frac{f(x_n)}{f'(x_n)}, \quad n=0,1,2,\dots.
$$

Under certain circumstances that we will not detail, the sequence \(\{x_n\}_{n=0}^{\infty}\) will converge to the root. Although the geometric interpretation is lost, the iterative method just described can also be used to find roots of functions of \(\mathbb{C}\) in \(\mathbb{C}\), and the same will be true hereafter. (In fact, it can also be adapted to find roots of functions defined on \(\mathbb{R}^d\), \(\mathbb{C}^d\), or even to Banach spaces, but that is outside the scope of what we want to expose here).

There are many other iterative methods for finding roots. For example, Halley’s method

$$
x_{n+1} = x_{n} – \frac{2 f(x_{n}) f'(x_{n})}{2(f'(x_{n}))^{2}-f(x_{n})f^{\prime\prime}(x_{n})}
$$
or Chebychev’s
$$
x_{n+1} = x_{n} –
\frac{f(x_{n})}{f'(x_{n})} \left(1+\frac{f(x_{n})f^{\prime\prime}(x_{n})}{2(f'(x_{n}))^{2}}\right).
$$

Quite a few more can be found in the book [6] or in the articles [3] or [7].

When these methods are applied to complex functions, the dynamics of iterative methods for solving equations can give rise to beautiful drawings (in addition to [1] or the aforementioned [7], it is also worth mentioning [5], which makes a more theoretical study), but this is not what we are concerned with here.

Since there are different methods with the same objective of finding roots of functions, it may be convenient to use one or the other depending on various circumstances. For example, the requirement on the initial point \(x_0\) to guarantee the convergence of the method to a root, the number of iterations required for the approximation to be good, the speed of execution of each step of the method, the stability, etc. An important criterion is the order of convergence. An iterative method \(x_{n+1} = I_f(x_{n})\) aimed at finding a simple root \(x^{*}\) of \(f\) is said to have order \(p>1\) if, after starting at a point \(x_0\) sufficiently close to \(x^{*}\), the following is satisfied

$$
\lim_{n \to \infty} \frac{|x^{*}-x_{n+1}|}{|x^{*}-x_{n}|^{p}} = C \neq 0.
$$

For example, Newton’s method has order \(2\), and Halley’s and Chebychev’s have order \(3\). In principle, the higher the order, the fewer iterations are needed to approximate \(x^{*}\) to the desired accuracy.

But, of course, we have to take into account the work it takes to perform each step of the method, and here it is essential to consider the number of evaluations of the function or its derivatives (we are assuming that, in principle, it takes the same amount of work to evaluate \(f\) as any of its derivatives involved in the iterative method). Newton’s method requires two evaluations, but Halley’s and Chebychev’s methods require three, so, in this sense, we cannot say that Halley’s and Chebychev’s are better methods than Newton’s, despite having a higher order of convergence.

It is easy to be convinced that, if we have an iterative method of order \(p\) and another of order \(q\), and in each step we apply them successively, we find a method of order \(pq\). For example, if in each step we apply Newton’s method twice, we have the following method of order \(4\):

$$
\begin{cases}
y_{n} = x_{n} – \frac{f(x_{n})}{f'(x_{n})}, \\[4pt]
x_{n+1} = y_{n} – \frac{f(y_{n})}{f'(y_{n})}.
\end{cases} 
$$
But in Newton’s method we evaluated \(f\) once and \(f’\) once, and now we are evaluating \(f\) twice and \(f’\) twice, so we are not gaining anything (the opposite would be miraculous). The good news is that the order \(4\) can be maintained by replacing one of these evaluations by some combination of the others. So, for example, we have Ostrowski’s method
$$
\begin{cases}
y_{n} = x_{n} – \frac{f(x_{n})}{f'(x_{n})}, \\[4pt]
x_{n+1} = y_{n} – \frac{f(y_{n})(y_{n}-x_{n})}{2 f(y_{n})-f(x_{n})}
\end{cases} 
$$

which is of order \(4\) and which, at each step, only evaluates \(f\) twice and \(f’\) once. In this sense, Ostrowski’s method is better than Halley’s and Chebychev’s methods because, with the same number of evaluations, it has a higher order of convergence.

If we combine Ostrowski’s and Newton’s methods we will have

$$
\begin{cases}
y_{n} = x_{n} – \frac{f(x_{n})}{f'(x_{n})}, \\[4pt]
z_{n} = y_{n} – \frac{f(y_{n})(y_{n}-x_{n})}{2 f(y_{n})-f(x_{n})}, \\[4pt]
x_{n+1} = z_{n} – \frac{f(z_{n})}{f'(z_{n})},
\end{cases} 
$$

a method of order \(8\) but with five evaluations of \(f\) or \(f’\). Again, one of the evaluations can be avoided by getting a \(8\)-order method that requires only four evaluations. It does not matter here how this is done; in fact, there are many, many iterative methods of order \(8\) with four evaluations, as can be seen in [1], which compares 29 such methods.

How far can this be achieved, and will it always be possible to eliminate an evaluation while maintaining the order, and how far can one go with \(d\) evaluations? Actually, it is not known, and the reader will have guessed that the Kung-Traub conjecture has an opinion on this.

To make things clear, we only need to give a couple of definitions. An iterative method is called memoryless when to calculate \(x_{n+1}\) it is only necessary to know \(x_n\), but not \(x_{n-1}\) or the previous ones; in this sense, the bisection or secant methods require memory (to perform a new step, we need the two previous points), but Newton’s method or the rest of the iterative methods we have seen here are memoryless methods. On the other hand, a method is called single-point if, at each step, the function and/or its derivatives are evaluated at a single point, and multi-point if they are evaluated at several points; for example, Newton’s, Halley’s and Chebychev’s methods are single-point (at each step, only \(f\) and the derivatives at \(x_{n}\) are evaluated), but Ostrowski’s is multi-point (evaluations are performed at \(x_{n}\) and at \(y_{n}\)).

In [6, Theorem 5-3], Traub had proved that a one-point method for solving a nonlinear equation of the form \(f(x) = 0\), which performs an evaluation of the given function \(f\) and of each of its \(p-1\) first derivatives, can attain at most order of convergence \(p\). This sparked interest in the study of multipoint methods, which were not constrained by this theoretical limit for the order of convergence, and therefore could allow for greater computational efficiency.

In 1974, Kung and Traub [2] stated what is now known as the Kung-Traub conjecture: a multipoint (and memoryless) iterative method for finding simple roots of a function can achieve at most order of convergence \(2^{d-1}\), where \(d\) is the total number of evaluations of the function or its derivatives.

Multipoint methods that satisfy the Kung-Traub conjecture are usually called optimal methods. For order \(2\), \(4\), \(8\) and \(16\), the optimal methods perform, respectively, \(2\), \(3\), \(4\) and \(5\) evaluations. It is proved theoretically that optimal methods exist for any number of \(d\) evaluations (see, for example, [2], [3, Section 3] or [4, Section 5]), but it is not ruled out that the order \(2^{d-1}\) can be exceeded.

To conclude, and in order to avoid any misunderstandings, I think it is important to make a few considerations about these very high order iterative methods. At large ranges, the order of the method being \(p\) means that the number of correct digits between the root \(x^{*}\) and its approximation \(x_n\) is multiplied by \(p\) in each iteration. Thus, high order methods provide, with very few iterations, an extraordinary accuracy for the root sought, with hundreds or thousands of correct digits, provided that we start from a point “close” to the root. The search for optimal methods has its undoubted theoretical interest, but, in practice, very high order methods are rarely required. It is often more reasonable to devote effort to trying to locate good starting points for the iterative method; or, from a theoretical point of view, to check conditions that guarantee the convergence of a method from sufficiently large starting areas. If a method has a very high order of convergence, but it is difficult to find a starting point that converges to the desired root, it is not going to be of much use in practice. But this is not what we were talking about here.

References

[1] C. Chun y B. Neta, Comparative study of eighth-order methods for finding simple roots of nonlinear equations, Numer. Algorithms 74 (2017), no. 4, 1169-1201.

[2] H. T. Kung y J. F. Traub, Optimal order of one-point and multipoint iteration, J. Assoc. Comput. Mach. 21 (1974), no. 4, 643-651.

[3] M. S. Petković, On a general class of multipoint root-finding methods of high computational efficiency, SIAM J. Numer. Anal. 47 (2010), no. 6, 4402-4414; Remarks on “On a general class of multipoint root-finding methods of high computational efficiency”, SIAM J. Numer. Anal. 49 (2011), no. 3, 1317-1319.

[4] M. S. Petković y L. D. Petković, Families of optimal multipoint methods for solving nonlinear equations: a survey, Appl. Anal. Discrete Math. 4 (2010), no. 1, 1-22.

[5] S. Plaza y J. M. Gutiérrez, Dinámica del método de Newton, Universidad de La Rioja, Logroño, 2013.

[6] J. F. Traub, Iterative Methods for the Solution of Equations, Prentice Hall, Englewood Cliffs, N.J., 1964.

[7] J. L. Varona, Graphic and numerical comparison between iterative methods, Math. Intelligencer 24 (2002), no. 1, 37-46.