Sendov conjecture

Among the simplest objects in mathematics are polynomials in one variable. Children study them in schools and high schools and, at least many of them, learn to operate with them and understand quite a few of their properties. Regarding the points at which polynomials cancel out (called zeros or roots), they know how to calculate them for polynomials of degrees 1 and 2, and for polynomials of higher degrees in some cases. They also study Bolzano’s theorem.

Si nos colocamos en un nivel académico más elevado, hay multitud de propiedades conocidas de los ceros de los polinomios. La más importante es que un polinomio de grado \(n\) tiene siempre exactamente \(n\) raíces complejas (contando su multiplicidad). Otros resultados bien conocidos son, por citar unos pocos, las fórmulas de Vieta-Cardano, la regla de los signos de Descartes y los teoremas de Sturm, Lagrange y Cauchy para localizar las raíces, el teorema de Gauss-Lucas sobre los ceros de la derivada, etcétera.

Pero lo que aquí nos interesa es que también existen propiedades que no se sabe si son ciertas o no. En matemáticas, normalmente no es fácil enunciar preguntas comprensibles por no especialistas cuya respuesta sea incierta. En esto, la teoría de números es una clara excepción, donde son numerosas las preguntas relativamente sencillas cuya respuesta no se conoce. Lo que ahora vamos a ver es un problema abierto relacionado con las raíces de polinomios y que, para comprender su enunciado, basta con conocer lo que es el plano complejo.

The problem came to the Bulgarian Blagovest Sendov in 1959. At the time, Sendov was a young professor of mathematics at the University of Sofia; in particular, he had specialised in numerical methods and computational mathematics. Years later he became rector of his university and a member of the Bulgarian Academy of Sciences; he also became interested in politics (he became president of the Bulgarian parliament), and was Bulgaria’s ambassador to Japan. He passed away in January 2020 (see [2]), so he did not have the chance to enjoy the pandemic that has now kept us all entertained. What Sendov surmised was the following:

Sendov conjecture (1959): Let \(f: \mathbb{C} \to \mathbb{C}\) be a polynomial of degree \(n \ge 2\) whose zeros are all on the (closed) unit circle; then, for any zero \(z_0\) of \(f(z)\), the (closed) circle of centre \(z_0\) and radius \(1\) contains at least one zero of the derivative \(f'(z)\).

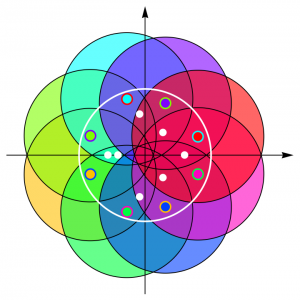
In the adjacent diagram you can see an example of the situation with the polynomial \(f(z) = z^8 – 17 z^4/72 + z^3/16 – z/12 + 81/256\), whose eight zeros, coloured, are all inside the unit circle (marked in white). Around each zero is shown, in the same colour as the zero, the circle of radius \(1\) centred on it. As can be seen, all these circles contain at least one of the seven zeros of \(f'(z)\), which are shown in white.

Sendov first passed on his conjecture to his colleague Nikola Obreshkov. It also reached the ears of Ljubomir Iliev, who, well connected with the mathematical community, discussed it with quite a few other mathematicians. In particular, he did so at a conference in Yerevan in 1965, quoting its author. We can imagine Iliev in the evening, having snacks in a bar after attending the conference talks, explaining the conjecture to a friend to see if they could come up with a counterexample or a proof. Thus the conjecture reached Walter Hayman, who included it in his book [1, Problem 4.5] (published in 1967); but Hayman had forgotten that the problem had been proposed by Sendov and attributed it to Iliev. This was the first time that the conjecture was put in writing, albeit under the name of the Iliev conjecture, by which it was known for several years (it is sometimes also called the Iliev-Sendov conjecture). More details of this story can be found in [3] and [2].

The Sendov conjecture remains an open problem, but since it was proposed there have been significant advances towards its solution. Some of these advances are worth mentioning:

• 1969: Amram Meir and Ambikeshwar Sharmaand proved the conjecture for polynomials of degree \(n \le 5\).
• 1991: Johnny E. Brown extends the proof to the case \(n \le 6\).
• 1996: Iulius Borcea gives another proof for the case \(n \le 6\), and proves also the case \(n \le 7\).
• 1997: Brown gives an indeependent proof for \(n \le 7\).
• 1999: Brown and his student Guangping Xiang reach the case \(n \le 8\).
• 2014: Jérôme Dégot proves that the conjecture is true for \(n\) slarge enough, but dependent of the zero \(z_0\).

Let us clarify a little more what the last point means. When we study the conjecture, we can consider that the polynomial is monic and rotate the zero \(z_0\) so that it is located in the interval \([0,1]\). In this way, we call the zero \(a\), and the conjecture can be analysed by making it depend on \(a\) (of course, the aim would be to prove it for all \(a\) and all \(n\)).

With this interpretation, the conjecture for \(a=0\) turns out to be the Gauss-Lucas theorem (the zeros of the derivative are in the convex envelope of the zeros of the polynomial). Likewise, Borislav Bojanov had shown in 2011 that the conjecture was true for \(a \le 1/(n-1)\); and Tomohiro Chijiwa that it was true for \(a \ge 1 – 1/(2^{2n+1}n^9)\) (Indraneel Kasmalkar extended this to \(a \ge 1 – 90/(n^{12}\log n)\) in 2014).

What Dégot proved in 2014 is that, for every \(c \in (0,1/2]\), and if the zero \(a\) satisfies \(c \le a \le 1-c\), the conjecture holds for \(n\) sufficiently large (dependent on \(c\)). In 2020, T. P. Chalebgwa extended the proof to the case \(C n^{-1/7} \le a \le 1 – Cn^{-1/4}\), for \(C\) a sufficiently large absolute constant.

In the above results the proof of Sendov’s conjecture for \(n\) sufficiently large was not very satisfactory, since it depended on the position of zero. For \(a\) very close to \(0\) or \(1\), the conjecture for \(n\) sufficiently large remained in doubt. It was at the end of 2020 that Terence Tao came on the scene. In his article [4], which for the moment is only published in arXiv, Tao once again surprises the mathematical community with a substantial advance, as he manages to prove that there exists an absolute constant \(n_0\) (i.e. without additional hypotheses about the position of zero) such that Sendov’s conjecture is true for polynomials of degree \(n \ge n_0\). In addition to [4], more details of Tao’s proof can be found in his blog [5].

Of course, there is still a long way to go before the proof is complete. In particular, although Tao proves the existence of the constant \(n_0\), he does not give an explicit value for this constant. Even so, the case \(9 \le n < n_0\) would still remain open. For how long?

References

[1] K. Hayman, Research Problems in Function Theory, Althlone Press, Londres, 1967.

[2] Ivanov y P. Petrushev, In Memoriam: Blagovest Sendov February 8, 1932-January 19, 2020, J. Approx. Theory 254 (2020), 105406, 27 pp.

[3] Bl. Sendov, Generalization of a conjecture in the geometry of polynomials, Serdica Math. J. 28 (2002), 283-304.

[4] T. Tao, Sendov’s conjecture for sufficiently high degree polynomials, arXiv:2012.04125, 2020, 36 pp.

[5] T. Tao, Sendov’s conjecture for sufficiently high degree polynomials, 8 de diciembre de 2020.